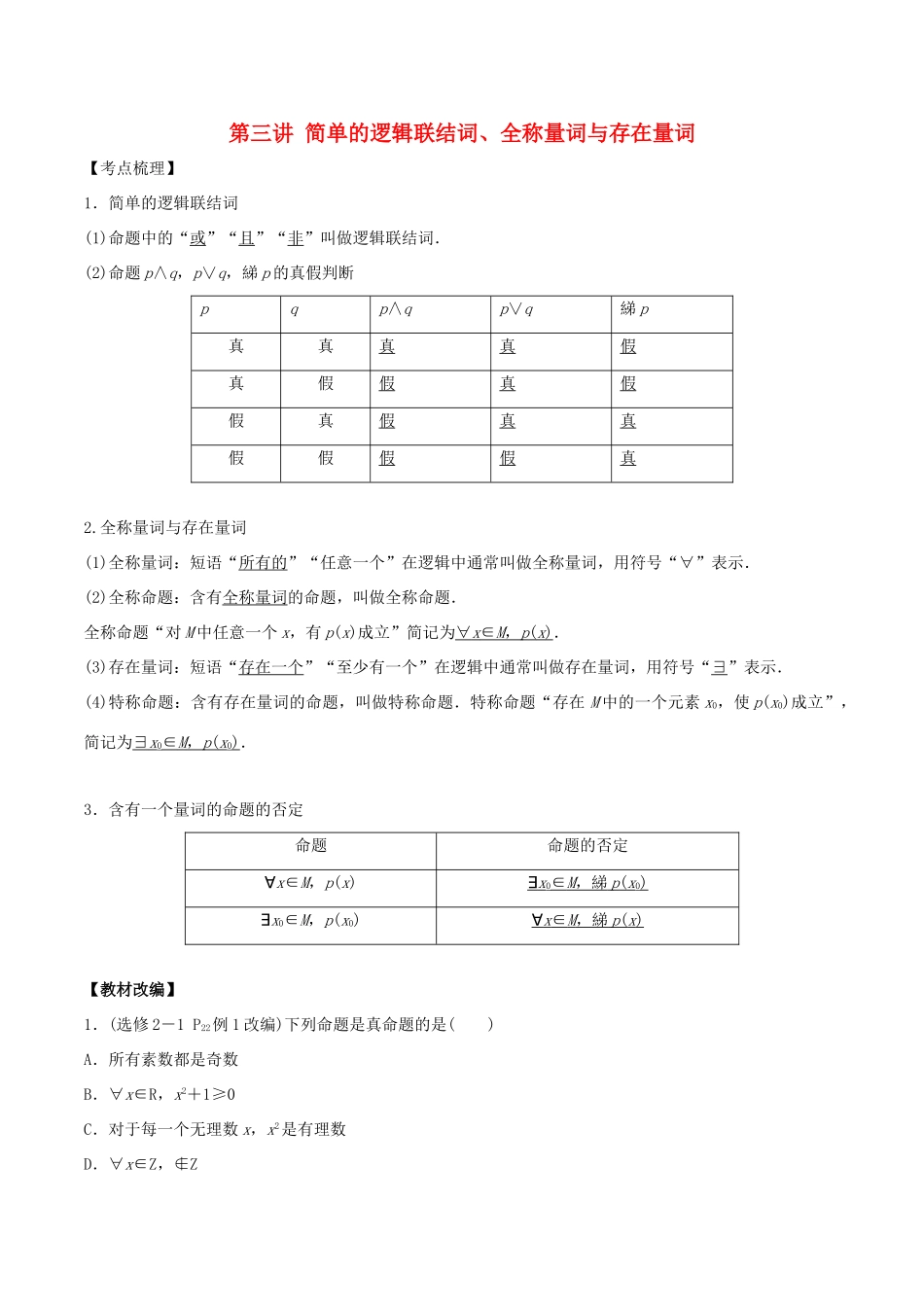
第三讲 简单的逻辑联结词、全称量词与存在量词【考点梳理】1.简单的逻辑联结词(1)命题中的“或”“且”“非”叫做逻辑联结词.(2)命题 p∧q,p∨q,綈 p 的真假判断pqp∧qp∨q綈 p真真真真假真假假真假假真假真真假假假假真2.全称量词与存在量词(1)全称量词:短语“所有的”“任意一个”在逻辑中通常叫做全称量词,用符号“”表示.∀(2)全称命题:含有全称量词的命题,叫做全称命题.全称命题“对 M 中任意一个 x,有 p(x)成立”简记为∀ x ∈ M , p ( x ) .(3)存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,用符号“∃”表示.(4)特称命题:含有存在量词的命题,叫做特称命题.特称命题“存在 M 中的一个元素 x0,使 p(x0)成立”,简记为∃ x 0∈ M , p ( x 0).3.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x)∃ x 0∈ M ,綈 p ( x 0)∃x0∈M,p(x0)∀ x ∈ M ,綈 p ( x ) 【教材改编】1.(选修 2-1 P22例 1 改编)下列命题是真命题的是( )A.所有素数都是奇数B.∀x∈R,x2+1≥0C.对于每一个无理数 x,x2是有理数D.∀x∈Z,∉Z【答案】 B2.(选修 2-1 P16例 3(1)改编)有下列两命题:①2≥2;② 2≥1,则下列正确的为( )A.①真②真 B.①真②假C.①假②真 D.①假②假【答案】 A【解析】 命题“2≥2”由命题 p:2=2,q:2>2 用“或”联结后构成的新命题,且 p 真 q 假,∴p∨q 为真,即①真,同理②也真,故选 A.3.(选修 2-1 P27 A 组 T3(3)改编)命题 p:∃x0∈R,x-x0+1≤0 的否定是( )A.∃x0∈R,x-x0+1>0B.∀x∈R,x2-x+1>0C.∃x0∈R,x-x0+1≥0D.∀x∈R,x2-x+1≤0【答案】 B【解析】 命题∃x0∈M,p(x0)的否定是∀x∈M,﹁p(x),故选 B.4.(选修 2-1 P27 A 组 T3(1)改编)命题 p:∀x∈N,x2>x3的否定是( )A.∃x0∈N,x>x B.∀x∈N,x2≤x3C.∃x0∈N,x≤x D.∀x∈N,x2<x3【答案】 C【解析】 命题∀x∈M,p(x)的否定是∃x0∈M,﹁p(x0),故选 C.5.(选修 2-1 P18 B 组 T(3)(4)改编)命题 p:2>3,q:8+7≠15,则“p∧q”的否定是( )A.2≤3 且 8+7=15 B.2≤3 或 8+7=15C.2>3 或 8+7≠15 D.2≤3 且 8+7≠15【答案】 B【解析】 因为“p∧q”的否定是“(﹁p)∨(﹁q)”,故选 B.【考点突破】考点一、含有逻辑联结词的命题的真...