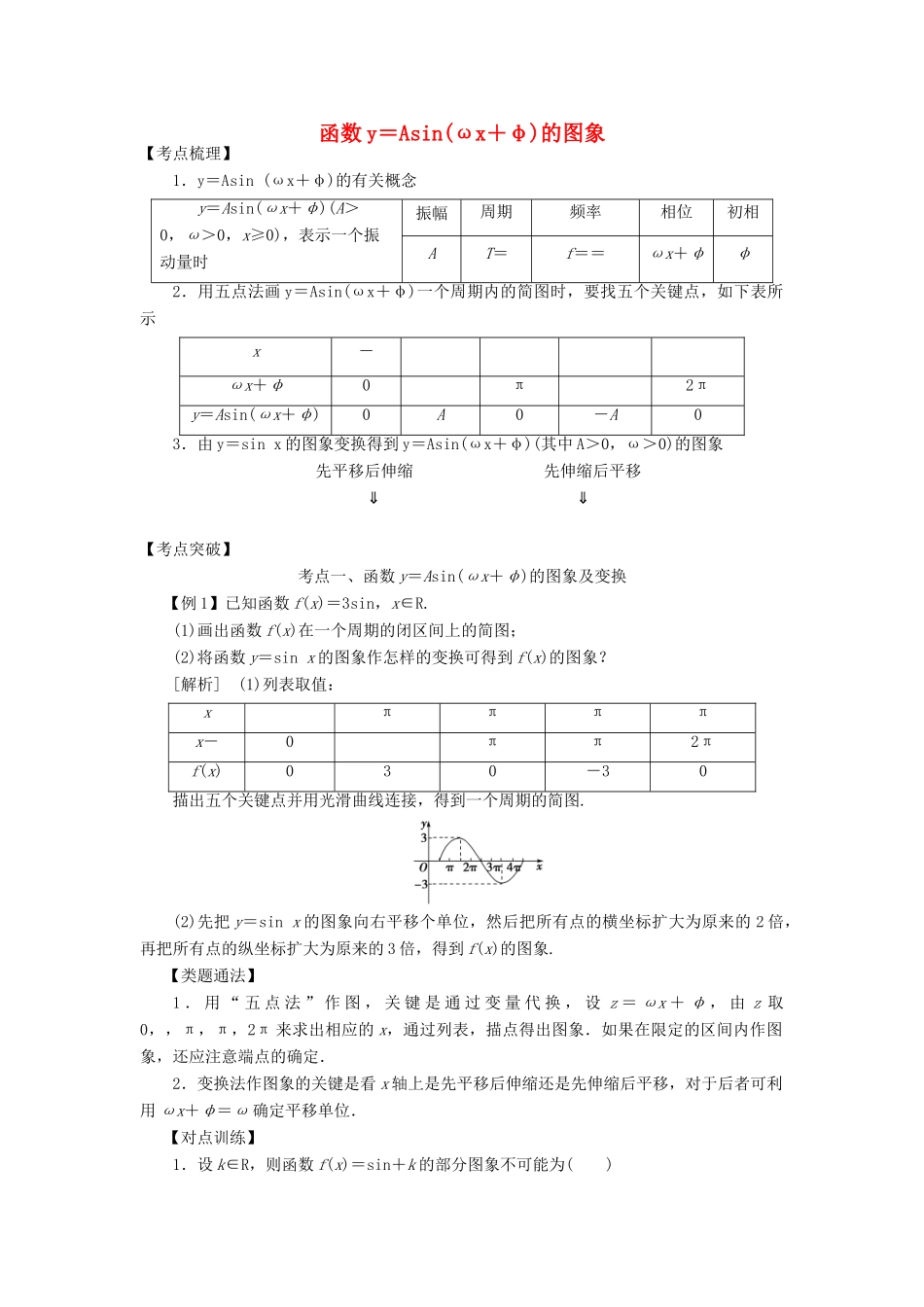
函数 y=Asin(ωx+φ)的图象【考点梳理】1.y=Asin (ωx+φ)的有关概念y=Asin(ωx+φ)(A>0,ω>0,x≥0),表示一个振动量时振幅周期频率相位初相AT=f==ωx+φφ2.用五点法画 y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示x-ωx+φ0π2πy=Asin(ωx+φ)0A0-A03.由 y=sin x 的图象变换得到 y=Asin(ωx+φ)(其中 A>0,ω>0)的图象先平移后伸缩 先伸缩后平移⇓ ⇓【考点突破】考点一、函数 y=Asin(ωx+φ)的图象及变换【例 1】已知函数 f(x)=3sin,x∈R.(1)画出函数 f(x)在一个周期的闭区间上的简图;(2)将函数 y=sin x 的图象作怎样的变换可得到 f(x)的图象?[解析] (1)列表取值:xππππx-0ππ2πf(x)030-30描出五个关键点并用光滑曲线连接,得到一个周期的简图.(2)先把 y=sin x 的图象向右平移个单位,然后把所有点的横坐标扩大为原来的 2 倍,再把所有点的纵坐标扩大为原来的 3 倍,得到 f(x)的图象.【类题通法】1 . 用 “ 五 点 法 ” 作 图 , 关 键 是 通 过 变 量 代 换 , 设 z = ωx + φ , 由 z 取0,,π,π,2π 来求出相应的 x,通过列表,描点得出图象.如果在限定的区间内作图象,还应注意端点的确定.2.变换法作图象的关键是看 x 轴上是先平移后伸缩还是先伸缩后平移,对于后者可利用 ωx+φ=ω 确定平移单位.【对点训练】1.设 k∈R,则函数 f(x)=sin+k 的部分图象不可能为( )[答案] D[解析] 当 k=0 时,f(x)=sin =,其图象为 A;当 k=2 时,f(x)=sin+2,其图象为 B;当 k=-1 时,f(x)=sin-1,其图象为 C;由选项 D 的图象可知 f(x)max=2,则 2=1+k⇒k=1.此时,f(x)=sin+1 的图象关于直线 x=对称,这与图象不符,故选 D.2.要得到函数 y=sin 的图象,只需将函数 y=sin 2x 的图象( )A.向左平移个单位 B.向右平移个单位C.向左平移个单位 D.向右平移个单位[答案] A[解析] 由 y=sin 2x 的图象得到 y=sin 的图象只需向左平移个单位,故选 A.考点二、由图象求函数 y=Asin(ωx+φ)的解析式【例 2】(1)函数 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数 f(x)的解析式为________.(2)函数 f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到 g(x)=Asin ωx 的图象,只需将函数...