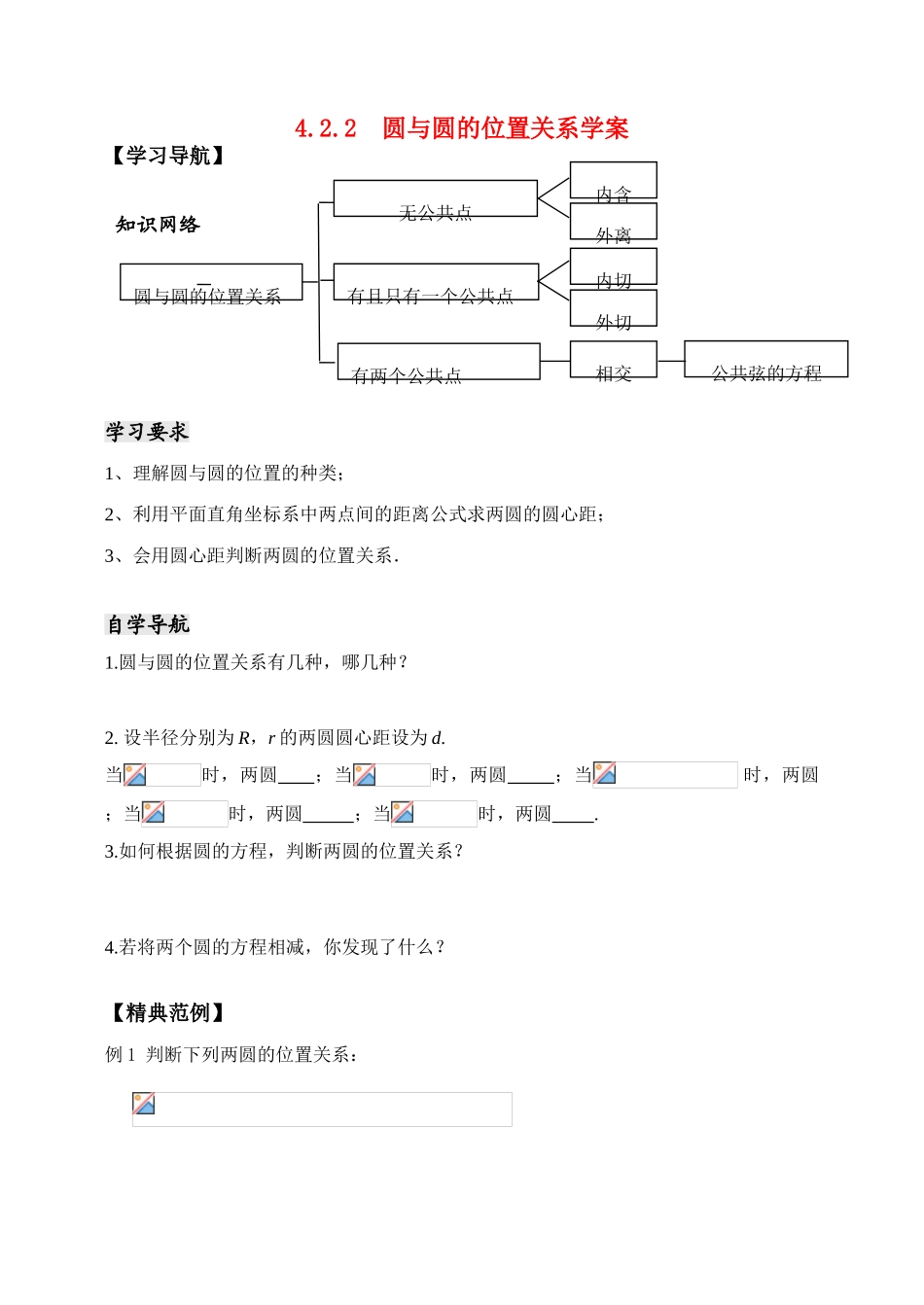
4.2.2 圆与圆的位置关系学案【学习导航】 知识网络 学习要求1、理解圆与圆的位置的种类;2、利用平面直角坐标系中两点间的距离公式求两圆的圆心距;3、会用圆心距判断两圆的位置关系.自学导航1.圆与圆的位置关系有几种,哪几种?2. 设半径分别为 R,r 的两圆圆心距设为 d.当时,两圆 ;当时,两圆 ;当 时,两圆 ;当时,两圆 ;当时,两圆 .3.如何根据圆的方程,判断两圆的位置关系?4.若将两个圆的方程相减,你发现了什么?【精典范例】例 1 判断下列两圆的位置关系: 有且只有一个公共点圆与圆的位置关系有两个公共点无公共点外离内含内切外切相交公共弦的方程 例 2 圆与圆相交于两点,求直线的 方程及公共弦的长. 例 3 求过点且与圆切于原点的圆的方程. 探究题 1:求过直线 x + y + 4 = 0 与圆 x2 + y2 + 4x – 2y – 4 = 0 的交点且与 y = x 相切的圆 的方程. 探究题 2:求过两圆 x2 + y2 + 6x – 4 = 0 求 x2 + y2 + 6y – 28 = 0 的交点,且圆心在直线 x – y – 4 = 0 上的圆的方程.【追踪训练】1.判断下列两个圆的位置关系:;.2.已知以 C(-4,3)为圆心的圆与圆相切,求圆 C 的方程.3. 若圆与圆相交,求实数的取值范围.4. 已知圆:和圆:,则当它们圆心之间的距离最短时,两圆的位置关系如何? 5.已知一个圆经过直线与圆的两个交点,并且有最小面积,求此圆的方程.6.已知圆,圆,求两圆的公共弦所在的直线方程及公共弦长.【反思与问题】1.我已掌握的知识和方法:2.我的疑问:分层训练1.已知,则两圆与的位置关系是 .2. 两圆与的公共弦长 .3.两圆相交于 A,B 两点,则直线 AB 的方程是 .4.已知两圆与,则 时,两圆相切.5.求经过点 M(2,-2),且与圆与交点的圆的方程.6.求过两圆和圆的交点,且圆心在直线 上的圆的方程.拓展延伸1.已知点,圆:,过 P 作圆 D,使 C 与 D 相切,并且使 D 的圆心坐标是正整数,求圆 D 的标准方程.2.已知两圆:, :.(1)求证两圆外切,且轴是它们的一条外公切线;(2)求出它的另一条外公切线方程.