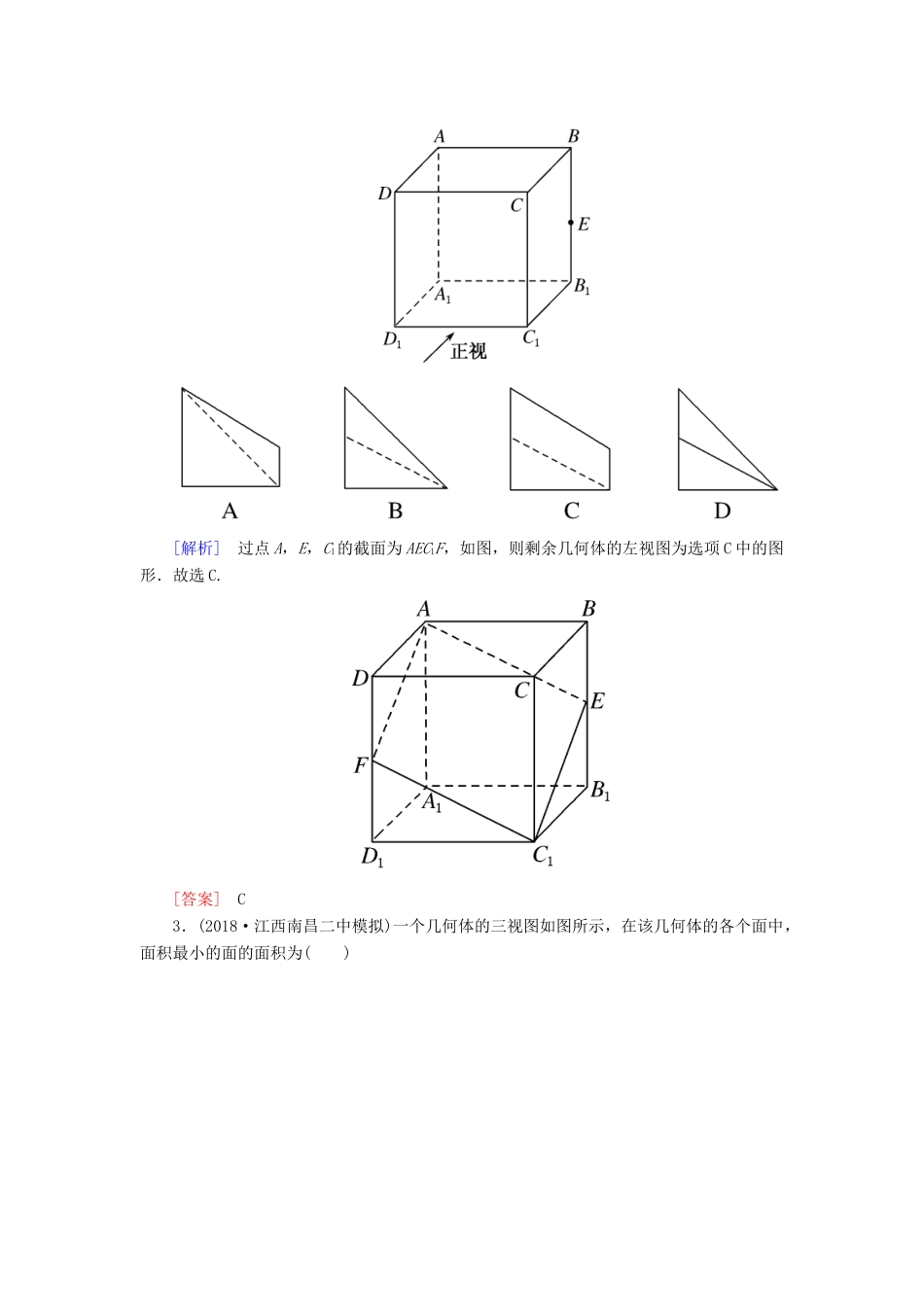
第一讲 空间几何体的三视图、表面积与体积考点一 空间几何体的三视图与直观图1.三视图的排列规则俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.2.原图形面积 S 与其直观图面积 S′之间的关系S′=S.[对点训练]1.(2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )[解析] 两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为 A.故选 A.[答案] A2.(2018·河北衡水中学调研)正方体 ABCD-A1B1C1D1中,E 为棱 BB1的中点(如图),用过点 A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为( )[解析] 过点 A,E,C1的截面为 AEC1F,如图,则剩余几何体的左视图为选项 C 中的图形.故选 C.[答案] C3.(2018·江西南昌二中模拟)一个几何体的三视图如图所示,在该几何体的各个面中,面积最小的面的面积为( )A.8 B.4 C.4 D.4[解析] 由三视图可知该几何体的直观图如图所示,由三视图特征可知,PA⊥平面ABC,DB⊥平面 ABC,AB⊥AC,PA=AB=AC=4,DB=2,则易得 S△PAC=S△ABC=8,S△CPD=12,S 梯形 ABDP=12,S△BCD=×4×2=4,故选 D.[答案] D4.如图所示,一个水平放置的平面图形的直观图是一个底角为 45°,腰和上底长均为 1 的等腰梯形,则该平面图形的面积为________.[解析] 直观图的面积 S′=×(1+1+)×=.故原平面图形的面积 S==2+.[答案] 2+[快速审题] (1)看到三视图,想到常见几何体的三视图,进而还原空间几何体.(2)看到平面图形直观图的面积计算,想到斜二侧画法,想到原图形与直观图的面积比为. 由三视图还原到直观图的 3 步骤(1)根据俯视图确定几何体的底面.(2)根据正(主)视图或侧(左)视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.(3)确定几何体的直观图形状.考点二 空间几何体的表面积与体积1.柱体、锥体、台体的侧面积公式(1)S 柱侧=ch(c 为底面周长,h 为高);(2)S 锥侧=ch′(c 为底面周长,h′为斜高);(3)S 台侧=(c+c′)h′(c′,c 分别为上下底面的周长,h′为斜高...