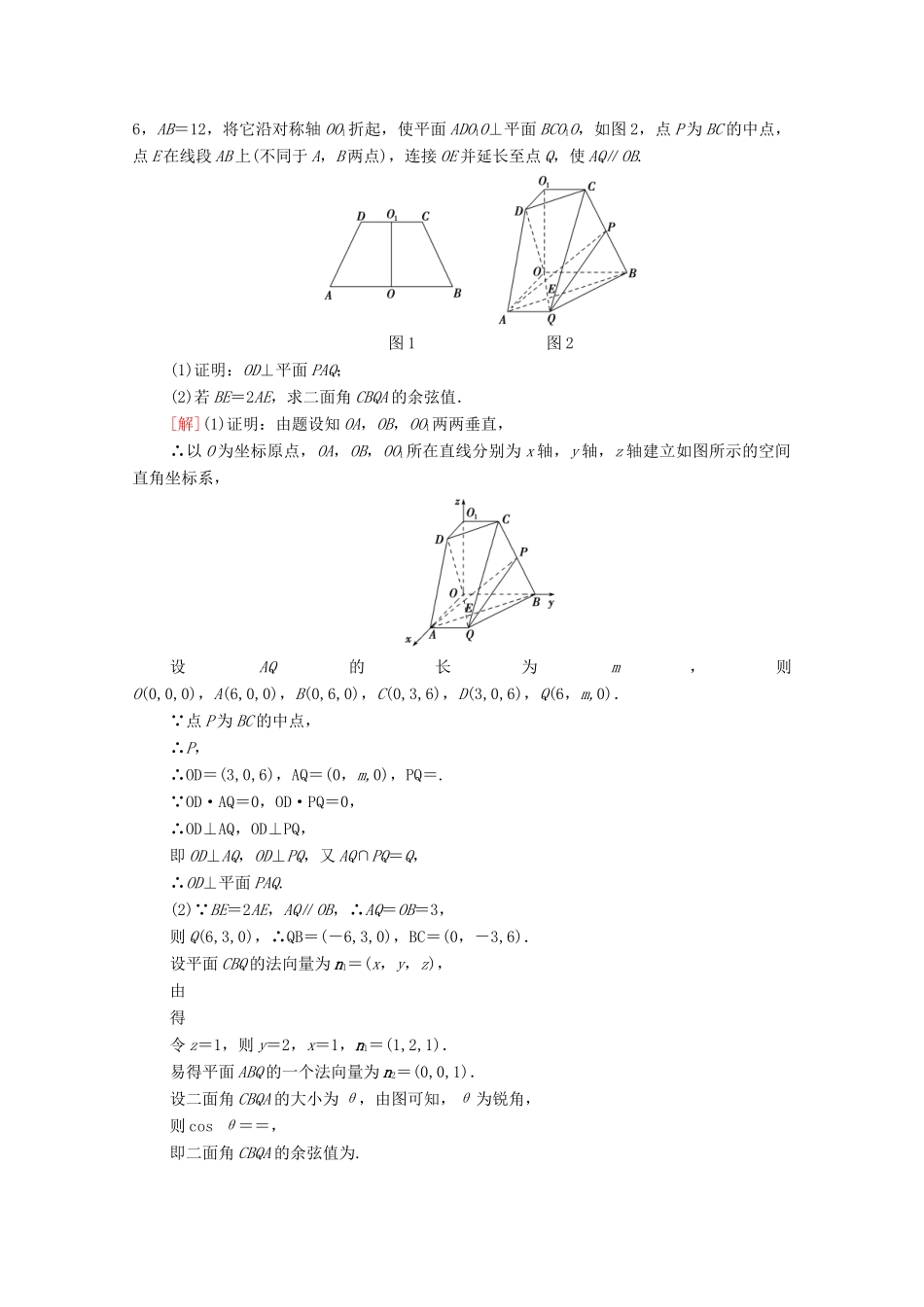
第七节 立体几何中的翻折、探究性、最值问题考点 1 平面图形的翻折问题 3 步解决平面图形翻折问题 (2018·全国卷Ⅰ)如图,四边形 ABCD 为正方形,E,F 分别为 AD,BC 的中点,以 DF 为折痕把△DFC 折起,使点 C 到达点 P 的位置,且 PF⊥BF.(1)证明:平面 PEF⊥平面 ABFD;(2)求 DP 与平面 ABFD 所成角的正弦值.[解](1)证明:由已知可得 BF⊥PF,BF⊥EF,PF∩EF=F,PF,EF⊂平面 PEF,所以 BF⊥平面 PEF.又 BF⊂平面 ABFD,所以平面 PEF⊥平面 ABFD.(2)如图,作 PH⊥EF,垂足为 H.由(1)得,PH⊥平面 ABFD.以 H 为坐标原点,HF的方向为 y 轴正方向,|BF|为单位长,建立如图所示的空间直角坐标系 Hxyz.由(1)可得,DE⊥PE.又 DP=2,DE=1,所以 PE=.又 PF=1,EF=2,所以 PE⊥PF.所以 PH=,EH=.则 H(0,0,0),P,D,DP=,HP=.又HP为平面 ABFD 的法向量,设 DP 与平面 ABFD 所成的角为 θ,则 sin θ=|cos〈HP,DP〉|===.所以 DP 与平面 ABFD 所成角的正弦值为. 平面图形翻折为空间图形问题重点考查平行、垂直关系,解题关键是看翻折前后线面位置关系的变化,根据翻折的过程找到翻折前后线线位置关系中没有变化的量和发生变化的量,这些不变的和变化的量反映了翻折后的空间图形的结构特征.[教师备选例题](2019·贵阳模拟)如图所示,在梯形 CDEF 中,四边形 ABCD 为正方形,且 AE=BF=AB=1,将△ADE 沿着线段 AD 折起,同时将△BCF 沿着线段 BC 折起,使得 E,F 两点重合为点 P.(1)求证:平面 PAB⊥平面 ABCD;(2)求直线 PB 与平面 PCD 的所成角的正弦值.[解](1)证明: 四边形 ABCD 为正方形,∴AD⊥AB,AD⊥AE,∴AD⊥AP, ∴AD⊥平面 PAB,又 AD⊂平面 ABCD,∴平面 ABCD⊥平面 PAB.(2)以 AB 中点 O 为原点,建立空间坐标系如图, AE=BF=AB=1,∴AP=AB=BP=1,∴B,P,C,D,∴PB=,DC=(1,0,0),CP=,设 n=(x,y,z)是平面 PCD 的一个法向量,则即取 z=2,则 n=(0,,2),设直线 PB 与平面 PCD 的所成角为 θ,则 sin θ=|cos〈n,PB〉|===,故直线 PB 与平面 PCD 的所成角的正弦值为. (2019·广州模拟)如图 1,在高为 6 的等腰梯形 ABCD 中,AB∥CD,且 CD=6,AB=12,将它沿对称轴 OO1折起,使平面 ADO1O⊥平面 BCO1O,如图 2,点 P 为 BC 的中点,点 E 在线段 AB 上(不同于 ...