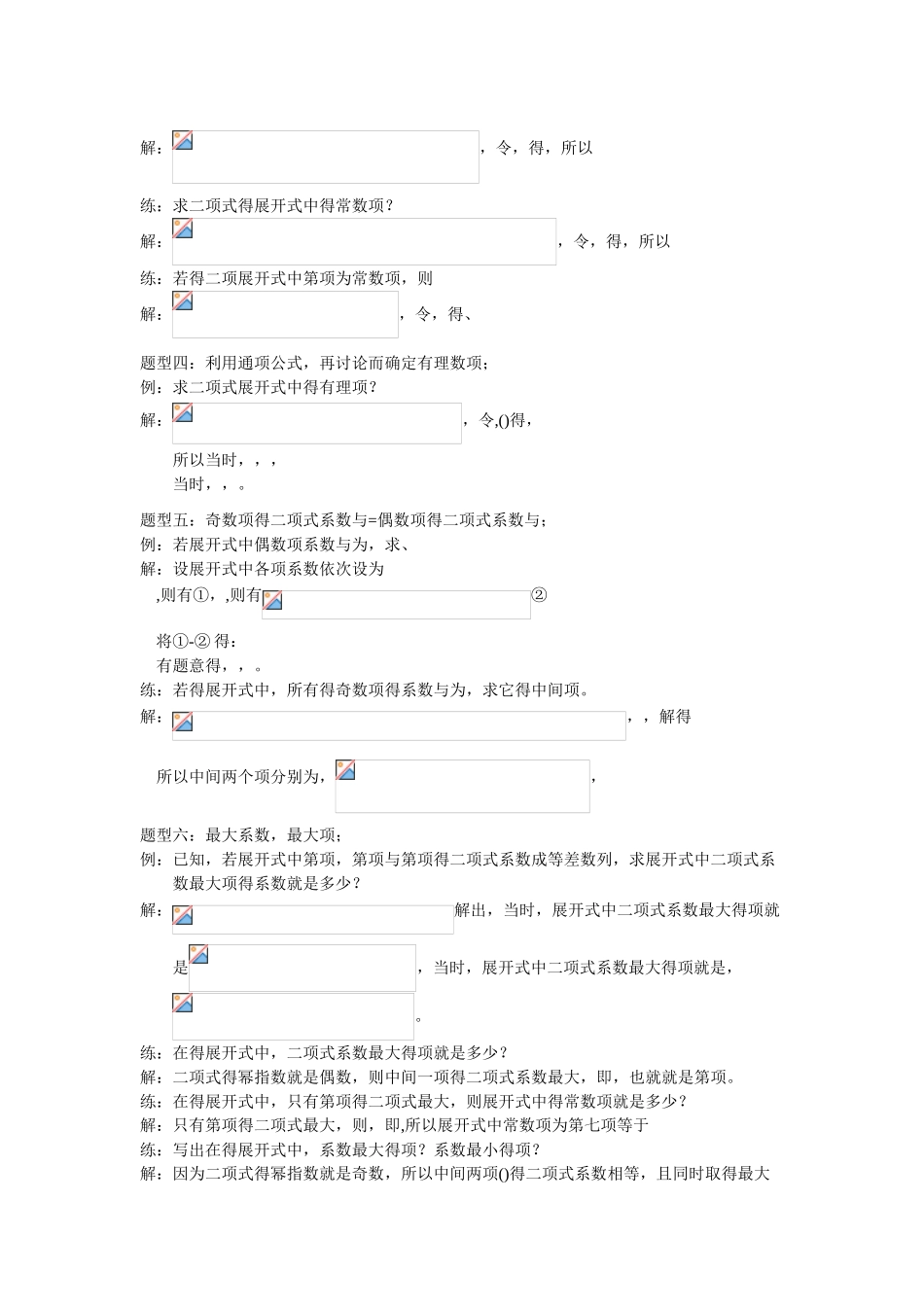
二项式定理1.二项式定理:,2.基本概念:① 二项式展开式:右边得多项式叫做得二项展开式。② 二项式系数:展开式中各项得系数、③ 项数:共项,就是关于与得齐次多项式④ 通项:展开式中得第项叫做二项式展开式得通项。用表示。3.注意关键点:① 项数:展开式中总共有项。② 顺序:注意正确选择,,其顺序不能更改。与就是不同得。③ 指数:得指数从逐项减到,就是降幂排列。得指数从逐项减到,就是升幂排列。各项得次数与等于、④ 系数:注意正确区分二项式系数与项得系数,二项式系数依次就是项得系数就是与得系数(包括二项式系数)。4.常用得结论:令 令 5.性质:① 二项式系数得对称性:与首末两端“对距离”得两个二项式系数相等,即,···② 二项式系数与:令,则二项式系数得与为, 变形式。③ 奇数项得二项式系数与=偶数项得二项式系数与:在二项式定理中,令,则,从而得到:④ 奇数项得系数与与偶数项得系数与:⑤ 二项式系数得最大项:假如二项式得幂指数就是偶数时,则中间一项得二项式系数取得最大值。 假如二项式得幂指数就是奇数时,则中间两项得二项式系数,同时取得最大值。⑥ 系数得最大项:求展开式中最大得项,一般采纳待定系数法。设展开式中各项系数分别为,设第项系数最大,应有,从而解出来。题型一:二项式定理得逆用;例:解:与已知得有一些差距, 练:解:设,则题型二:利用通项公式求得系数;例:在二项式得展开式中倒数第项得系数为,求含有得项得系数?解:由条件知,即,,解得,由,由题意,则含有得项就是第项,系数为。练:求展开式中得系数?解:,令,则故得系数为。题型三:利用通项公式求常数项;例:求二项式得展开式中得常数项?解:,令,得,所以练:求二项式得展开式中得常数项?解:,令,得,所以练:若得二项展开式中第项为常数项,则解:,令,得、题型四:利用通项公式,再讨论而确定有理数项;例:求二项式展开式中得有理项?解:,令,()得,所以当时,,,当时,,。题型五:奇数项得二项式系数与=偶数项得二项式系数与;例:若展开式中偶数项系数与为,求、解:设展开式中各项系数依次设为 ,则有①,,则有② 将①-② 得: 有题意得,,。练:若得展开式中,所有得奇数项得系数与为,求它得中间项。解:,,解得 所以中间两个项分别为,,题型六:最大系数,最大项;例:已知,若展开式中第项,第项与第项得二项式系数成等差数列,求展开式中二项式系数最大项得系...