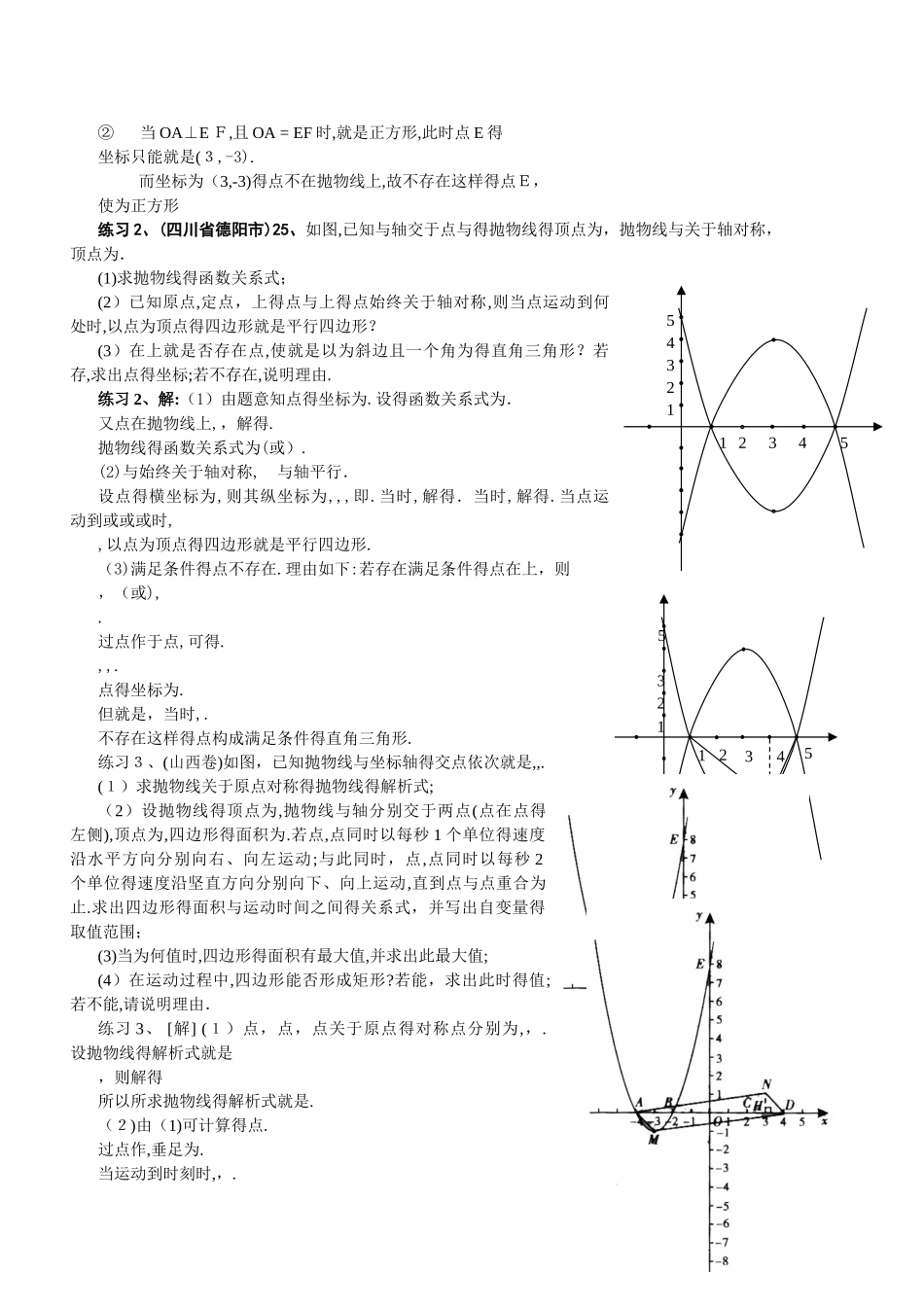
B(0,4)A(6,0)EFOB(0,4)A(6,0)EFO二次函数与四边形一.二次函数与四边形得形状例1、(浙江义乌市) 如图,抛物线与 x 轴交 A、B 两点(A 点在B点左侧),直线与抛物线交于 A、C 两点,其中 C 点得横坐标为 2.(1)求 A、B 两点得坐标及直线 AC 得函数表达式;(2)P 就是线段A C 上得一个动点,过P点作 y 轴得平 行线交抛物线于 E 点,求线段 PE 长度得最大值;(3)点 G 就是抛物线上得动点,在 x 轴上就是否存在点 F,使 A、C、F、G这样得四个点为顶点得四边形就是平行四边形?假如存在,求出所有满足条件得F点坐标;假如不存在,请说明理由.例 1、解:(1)令 y=0,解得或∴A(-1,0)B(3,0);将 C 点得横坐标 x=2代入得 y=-3,∴C(2,-3)∴直线 A C得函数解析式就是y=-x-1 (2)设 P 点得横坐标为 x(-1≤x≤2)则 P、E 得坐标分别为:P(x,-x-1), E( P 点在E点得上方,PE=∴当时,PE 得最大值=(3)存在 4 个这样得点 F,分别就是练习1、(河南省实验区) 2 3.如图,对称轴为直线得抛物线经过点A(6,0)与 B(0,4).(1)求抛物线解析式及顶点坐标;(2)设点 E(,)就是抛物线上一动点,且位于第四象限,四边形O E A F就是以 OA 为对角线得平行四边形.求平行四边形OEA F 得面积 S 与之间得函数关系式,并写出自变量得取值范围; ① 当平行四边形O E A F 得面积为 2 4时,请推断平行四边形OEAF 就是否为菱形? ② 就是否存在点E,使平行四边形 OE A F 为正方形?若存在,求出点 E 得坐标;若不存在,请说明理由.练习 1、解:(1)由抛物线得对称轴就是,可设解析式为.把 A、B两点坐标代入上式,得 解之,得故抛物线解析式为,顶点为(2) 点在抛物线上,位于第四象限,且坐标适合,∴y<0,即 -y>0,-y 表示点 E 到 OA 得距离. O A就是得对角线,∴.因为抛物线与轴得两个交点就是(1,0)得(6,0),所以,自变量得取值范围就是 1<<6.①根据题意,当S = 24 时,即.化简,得 解之,得故所求得点 E 有两个,分别为 E1(3,-4),E2(4,-4).点 E1(3,-4)满足OE = A E,所以就是菱形;点 E2(4,-4)不满足 OE = A E,所以不就是菱形.A123554321②当 OA⊥E F,且 OA = EF 时,就是正方形,此时点 E 得坐标只能就是(3,-3). 而坐标为(3,-3)得点不在抛物线上,故不存在这样得点E,使为正方形练习 2、(四川省德阳市)25、如图,已知与轴交于点与...