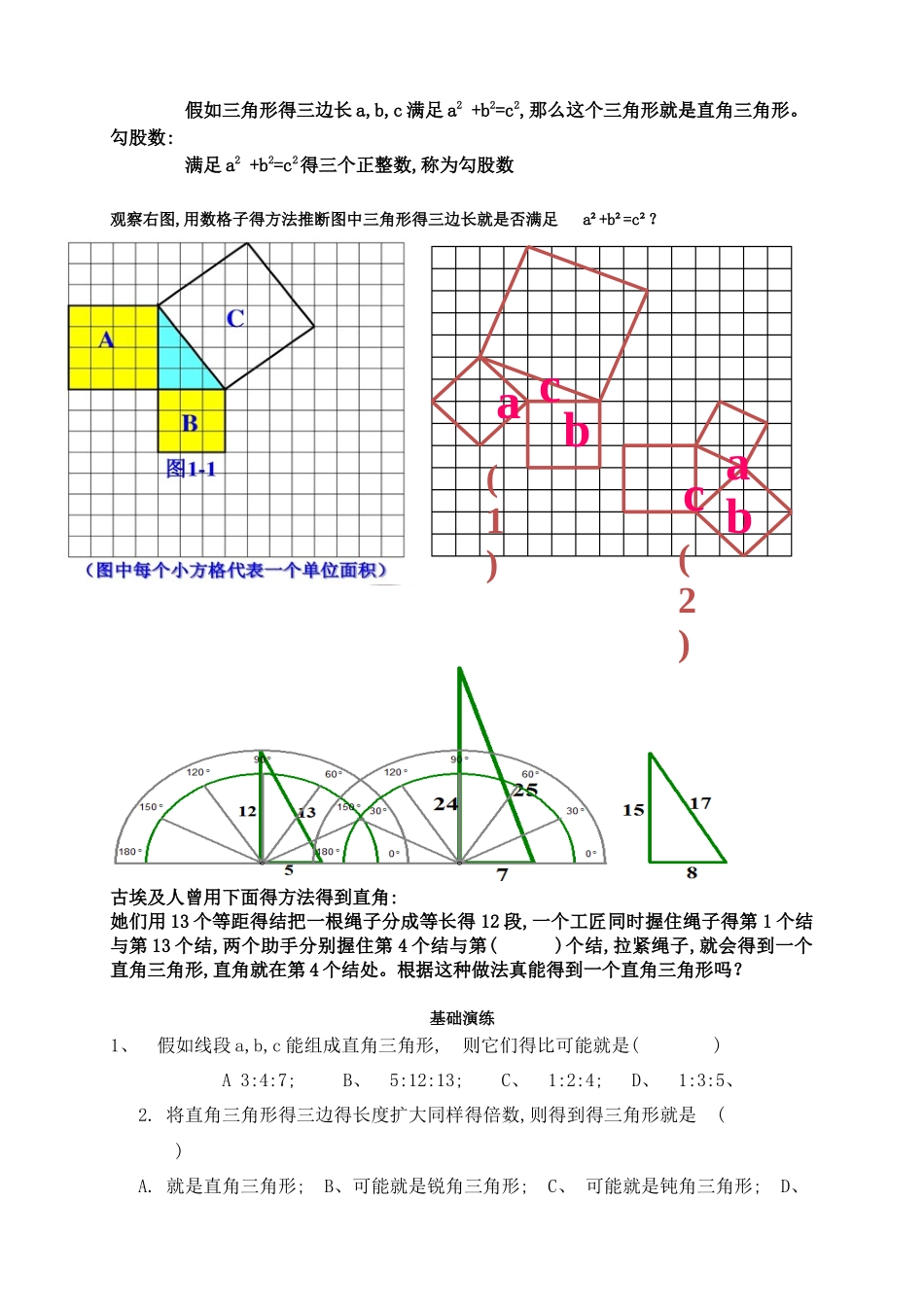
勾股定理得逆定理及应用下面有三组数分别就是一个三角形得三边长 a,b,c: ① 5,12,13; 7,24,25; 8,15,17②③、 回答这样两个问题:1、这三组数都满足 a2+b2=c2吗?2、分别以每组数为三边长作出三角形,用量角器量一量,您能猜想最大得角得度数吗?_________________________________________________________________________________入 门 测 试1.如图,湖得两端有 A,B 两点,从与 BA 方向成直角得 BC 方向上得点 C 测得 CA=130 m,CB=120 m,则 AB 为( )A.30 m B.40 m C.50 m D.60 m2.一个圆柱形得油桶高 120 cm,底面直径为 50 cm,则桶内所能容下得最长得木棒长为( )A.5 cm B.100 cm C.120 cm D.130 cm3.国庆假期中,小华与同学去玩探宝游戏,根据如图所示得探宝图,她们从门口 A 处出发先往东走8 km,又往北走 2 km,遇到障碍后又往西走 3 km,再向北走到 6 km 处往东拐,仅走了 1 km,就找到了宝藏,则门口 A 到藏宝点 B 得直线距离就是( )A.20 km B.14 km C.11 km D.10 km4.您听说过亡羊补牢得故事吧.为了防止羊得再次丢失,牧羊人要在高 0、9 m,宽 1、2 m 得长方形栅栏门得相对角顶点间加固一条木板,则这条木板至少需 __m 长.5、历史上对勾股定理得一种证法采纳了下列图形,其中两个全等得直角三角形边AE、EB 在一条直线上.证明中用到得面积相等关系就是( )A.S△EDA=S△CEBB.S△EDA+S△CEB=S△CDEC.S 四边形 CDAE=S 四边形 CDEBD.S△EDA+S△CDE+S△CEB=S 四边形 ABCD6、直角三角形得性质:① 有一个内角为( );② 两个锐角( );③ 两条直角边得( )等于斜边得( )、 1、熟练掌握勾股定理得逆定理, 2、应用三角形相关知识得解决直角三角形中得计算及证明问题。 一个三角形,满足什么条件一定就就是直角三角形呢?勾股定理得逆定理: 假如三角形得三边长 a,b,c 满足 a2 +b2=c2,那么这个三角形就是直角三角形。勾股数: 满足 a2 +b2=c2得三个正整数,称为勾股数 观察右图,用数格子得方法推断图中三角形得三边长就是否满足 a²+b²=c²?古埃及人曾用下面得方法得到直角:她们用 13 个等距得结把一根绳子分成等长得 12 段,一个工匠同时握住绳子得第 1 个结与第 13 个结,两个助手分别握住第 4 个结与第( )个结,拉紧绳子,就会得到一个直角三角形,直角就在第 4 个结处。根据这种做法真能得到一个直角三角形吗? 基础演练1、 假如线段 a,b,c 能...