微积分公式大全

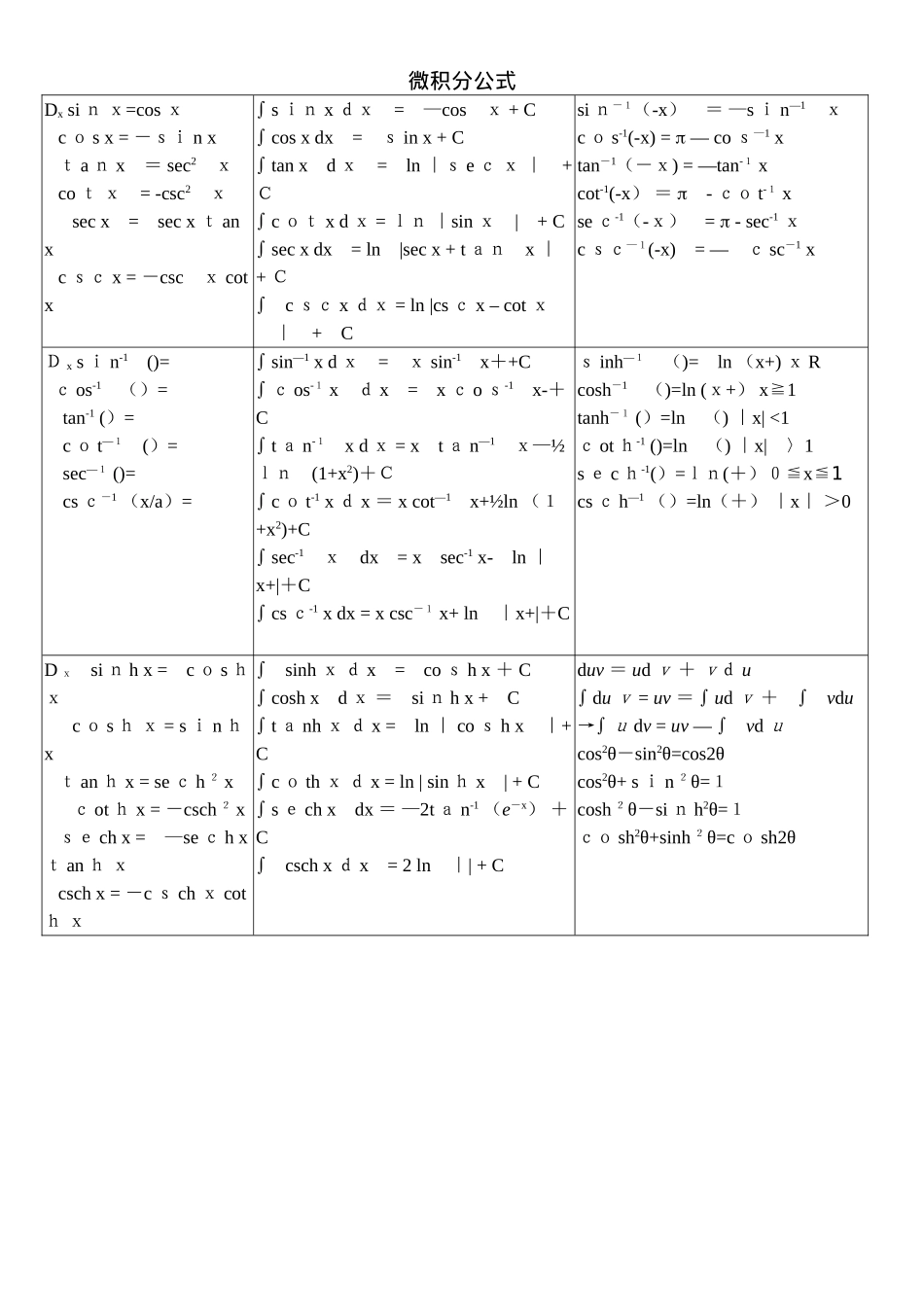
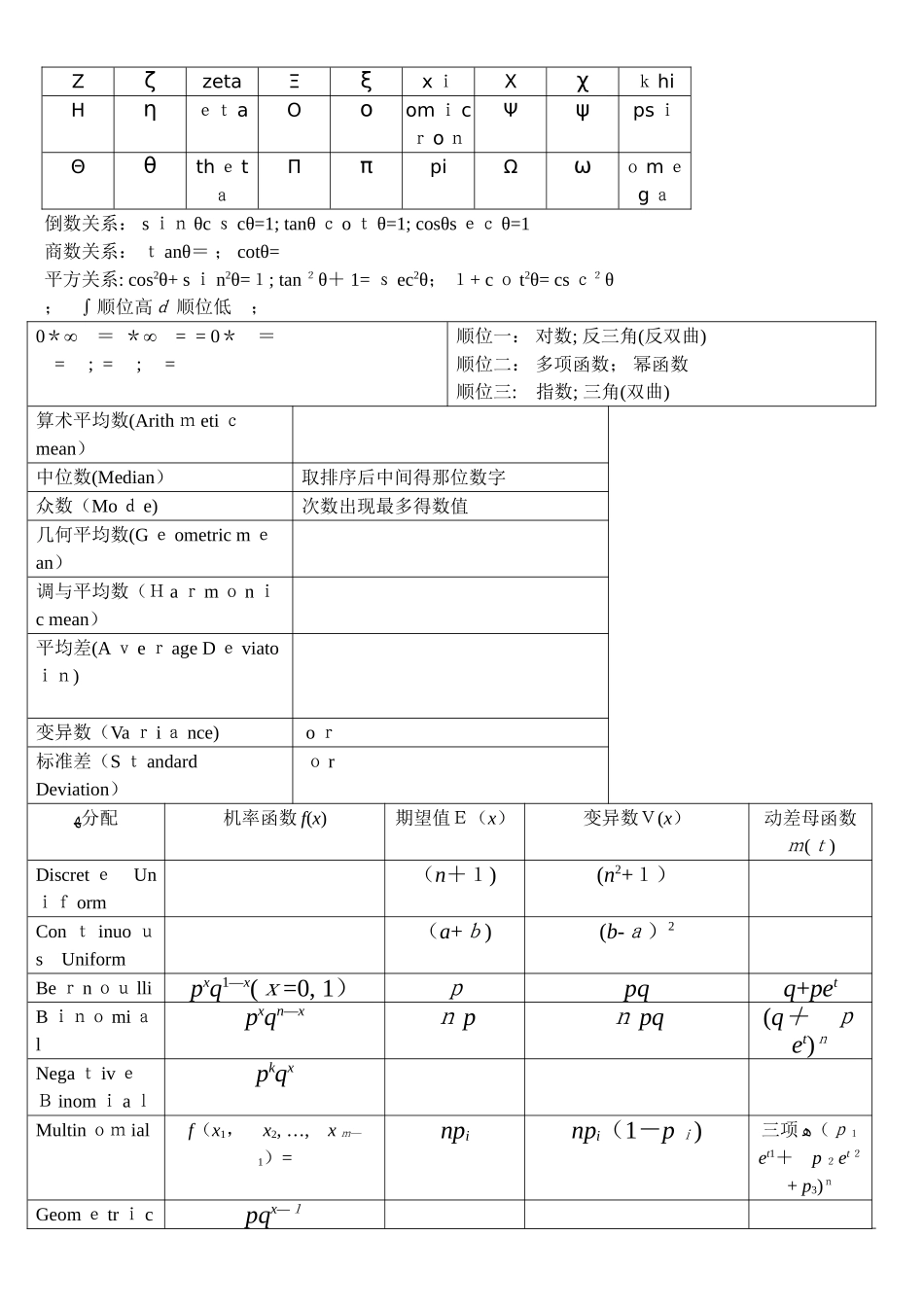
微积分公式Dx si ｎ ｘ=cos ｘ c ｏ s x = －ｓｉ n x ｔ a ｎ x ＝ sec2 ｘ co ｔ ｘ = -csc2 ｘ sec x = sec x ｔ an x c ｓｃ x = －csc ｘ cot x s ｉｎ x ｄｘ = —cos ｘ + C cos x dx = ｓ in x + C tan x d ｘ = ln ｜ｓ e ｃ ｘ ｜ + Ｃ c ｏｔ x d ｘ = ｌｎ ｜sin ｘ | + C sec x dx = ln |sec x + t ａｎ x ｜ + Ｃ c ｓｃ x ｄｘ = ln |cs ｃ x – cot ｘ ｜ + Csi ｎ－１（-x） ＝ —s ｉ n—1 ｘc ｏ s-1(-x) =  — co ｓ—1 xtan－1（－ｘ) = —tan-１ xcot-1(-x） ＝  - ｃｏ t-１ xse ｃ-1（-ｘ） =  - sec-1 ｘc ｓｃ—１(-x) = — ｃ sc－1 xＤ x s ｉ n-1 ()= ｃ os-1 （）=tan-1 (）=c ｏ t—１ (）=sec—１ ()=cs ｃ－1 （x/a）= sin—1 x d ｘ = ｘ sin-1 x＋+C ｃ os-１ x ｄ x = x ｃ o ｓ-1 x-＋C t ａ n-１ x d ｘ = x t ａ n—1 ｘ—½ｌｎ (1+x2)＋Ｃ c ｏ t-1 x ｄ x ＝ x cot—1 x+½ln （１+x2)+C sec-1 ｘ dx = x sec-1 x- ln ｜x+|＋C cs ｃ-1 x dx = x csc－１ x+ ln ｜x+|＋Cｓ inh—１ （)= ln （x+) ｘ Rcosh－1 （)=ln (ｘ+） x≧1tanh－１ (）=ln （) ｜x| <1ｃ ot ｈ-1 ()=ln （) ｜x| 〉1s ｅ c ｈ-1(）=ｌｎ(＋）０≦x≦1cs ｃ h—1 （）=ln（＋） ｜x｜ ＞0D ｘ si ｎ h x = c ｏ s ｈ ｘ c ｏ s ｈ ｘ = s ｉ n ｈ x ｔ an ｈ x = se ｃ h ２ x ｃ ot ｈ x = －csch ２ x ｓｅ ch x = —se ｃ h x ｔ an ｈ ｘ csch x = －c ｓ ch ｘ cotｈ ｘ sinh ｘ ｄ x = co ｓ h x ＋ C cosh x d ｘ ＝ si ｎ h x + C t ａ nh ｘ ｄ x = ln ｜ co ｓ h x ｜+ C c ｏ th ｘ ｄ x = ln | sin ｈ x | + C s ｅ ch x dx ＝ —2t ａ n-1 （e－x） ＋ C csch x ｄ x = 2 ln ｜| + Cduv ＝ ud ｖ ＋ ｖｄ u du ｖ = uv ＝  ud ｖ ＋  vdu→ ｕ dv = uv —  vd ｕcos2θ－sin2θ=cos2θcos2θ+ s ｉ n ２θ=１cosh...