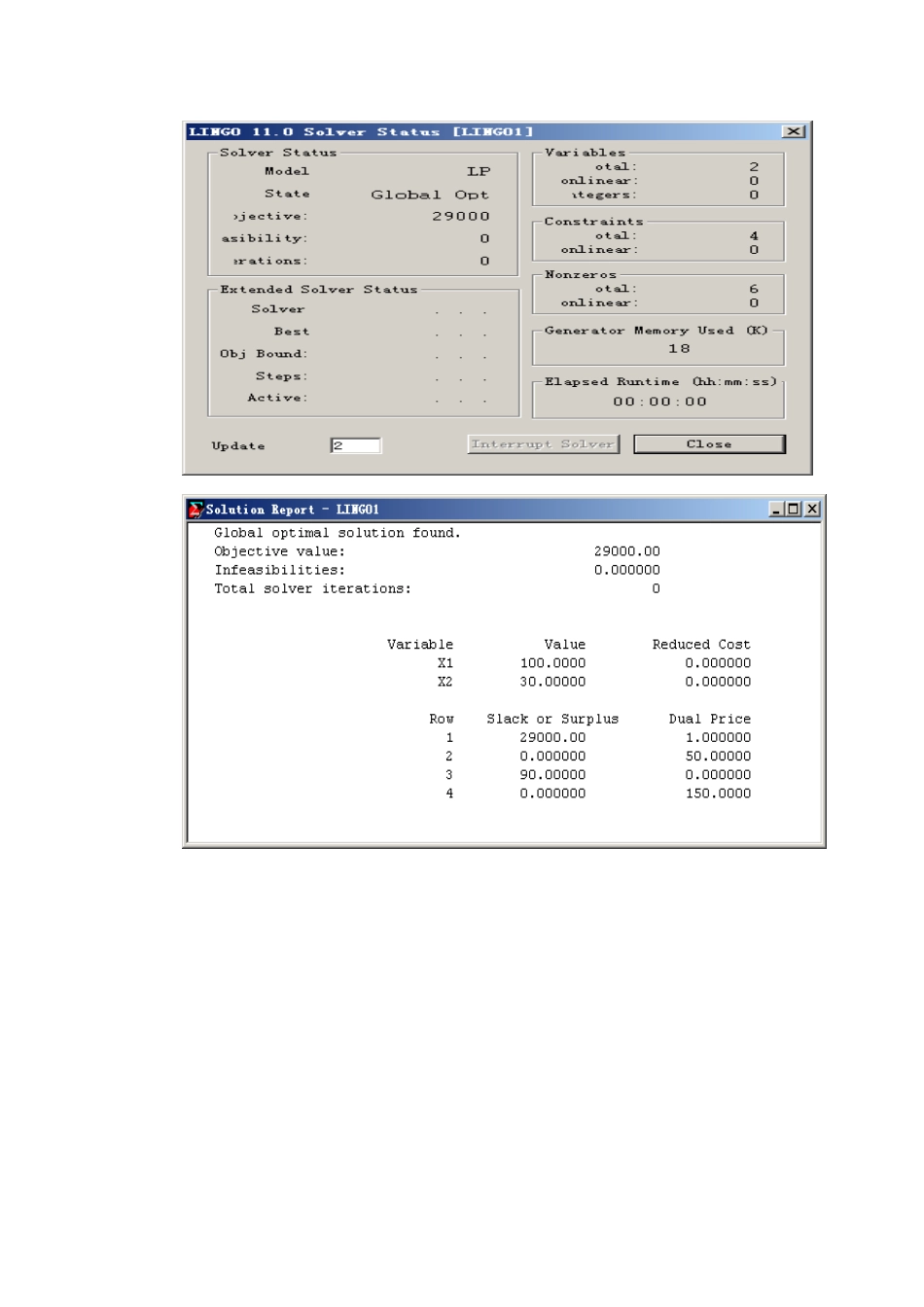
经过一个学期数学建模得学习,学到了很多,收获也很多,老师们得精彩讲课,让我感受到了老师们得热情以及对学术得尊敬,也让我陶醉在数学建模这门深奥而又让人着迷于这门科学,在此,感谢老师得栽培与培育。接下来让我谈谈对数学建模得理解.在我瞧来,数学建模属于一门应用数学,学习这门课要求我们学会如何将实际问题经过分析、简化转化为一个数学问题,然后用适当得数学方法去解决。数学建模就是一种数学得思考方法,就是运用数学得语言与方法,通过抽象、简化建立能近似刻画并”解决”实际问题得一种强有力得数学手段。为了使描述更具科学性,逻辑性,客观性与可重复性,人们采纳一种普遍认为比较严格得语言来描述各种现象,这种语言就就是数学.使用数学语言描述得事物就称为数学模型。 数学建模广泛涉猎课外知识、利用数学与计算机工具、为某一具体问题建立抽象模型、给出求解方法并解决问题、最后撰写论文并给出客观评价得一个系统工程。数学建模就就是利用数学知识对一些实际问题建立模型,但又不就是纯数学得。它不仅要数学思维,还要计算机编程能力,论文写作能力,其实更重要得就是团队协作能力,这就是对以后工作有非常大得帮助得,更甚就是人生。第一、 通过这学期学得题目来体现我对数学建模得理解,由于一个学期得笔记太多,现在我就用一道题来表达一下数学建模得应用例:工厂有两条生产线,分别生产 M 与 P 两种型号得产品,利润分别为 200 元/个与 30 0元/个,生产能力分别为 10 0与 120,生产一个产品分别需1个与 2 个劳动日,工厂每天能提供 160 个劳动日。假设原材料不受限制,如何安排生产计划,利润最大。 设生产计划为生产 x1 个M与x 2 个 P,数学模型为由此瞧出,数学建模就就是运用数学实现模型化,运用数学理论,公式,定律,定理,函数等数学物理知识来实现,求得最我们想要得最大值或者最小值以及通过模型来实现趋势得预测.其中最重要得就是把握好约束条件,约束不同,一般所得到得模型也不同,预测得结果也不同。第二、这学期我们还学会了数学建模软件,运用数学建模软件来提高我们得效率,有效得实现复杂函数电子显示。例如 lingo 软件,ex c e l软件等,就上题我们可以运用 ling o软件这样求得L I NGO 求解1、输入模型 2、模型存盘存为、lg 4 文件 3、模型求解 选 Lingo|Solve(C t r l+s) 就这样我们得到了想要得结果,由此可见 l i ngo 软件对我们数学建模十分重要...