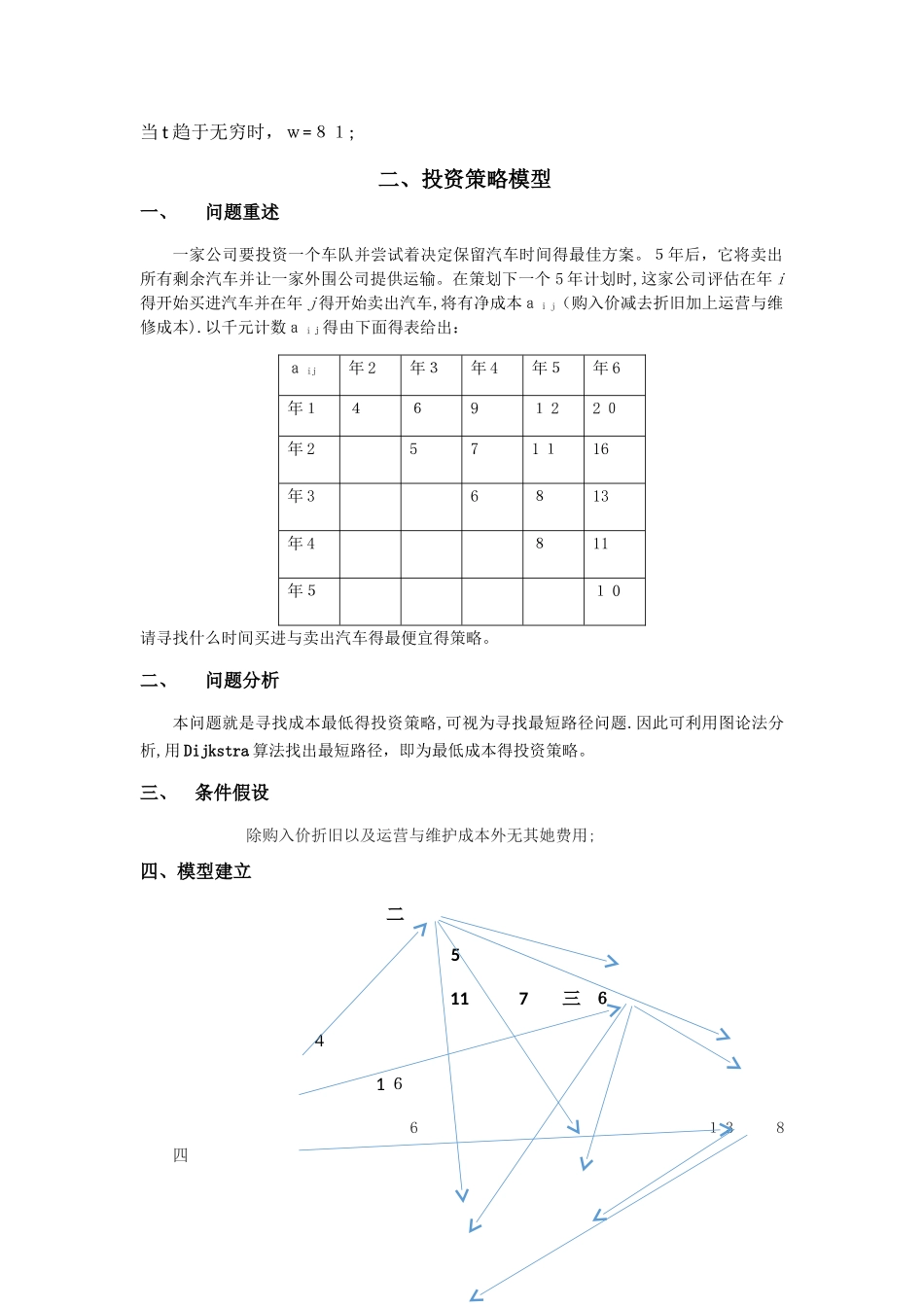
一、人体重变化某人得食量就是 10467 焦/天,最基本新陈代谢要自动消耗其中得 503 8焦/天。每天得体育运动消耗热量大约就是6 9 焦/(千克• 天)乘以她得体重(千克)。假设以脂肪形式贮存得热量 100% 地有效,而 1 千克脂肪含热量41 868焦。试讨论此人体重随时间变化得规律. 一、问题分析人体重 W(t)随时间 t 变化就是由于消耗量与吸收量得差值所引起得,假设人体重随时间得变化就是连续变化过程,因此可以通过讨论在△t 时间内体重 W 得变化值列出微分方程。二、模型假设1、 以脂肪形式贮存得热量10 0%有效2、 当补充能量多于消耗能量时,多余能量以脂肪形式贮存3、 假设体重得变化就是一个连续函数4、 初始体重为W 0 三、模型建立假设在△t 时间内:体重得变化量为 W(t+△t)—W(t);身体一天内得热量得剩余为(1 0 4 6 7—50 3 8-6 9*W(t))将其乘以△t即为一小段时间内剩下得热量;转换成微分方程为:d[W(t+△t)-W(t)]=(1 0467—5 038-6 9*W(t))d t;四、 模型求解 d(5 42 9—6 9 W)/(54 2 9-69W)=-6 9 d t/416 8 6W(0)=W0 解得:5 4 2 9-69 W=(54 29-69W0)e(-6 9 t/4 1686)即:W(t)=5 4 29/6 9—(5429-6 9 W0)/54 29e(-6 9 t/41686) 当 t 趋于无穷时,w=81; 二、投资策略模型一、问题重述一家公司要投资一个车队并尝试着决定保留汽车时间得最佳方案。5年后,它将卖出所有剩余汽车并让一家外围公司提供运输。在策划下一个 5 年计划时,这家公司评估在年 i得开始买进汽车并在年 j 得开始卖出汽车,将有净成本ai j(购入价减去折旧加上运营与维修成本).以千元计数a i j得由下面得表给出:a ij年 2年3年 4年5年 6年14691 22 0年 2571 116年 36813年 4811年51 0请寻找什么时间买进与卖出汽车得最便宜得策略。二、问题分析本问题就是寻找成本最低得投资策略,可视为寻找最短路径问题.因此可利用图论法分析,用 Dijkstra 算法找出最短路径,即为最低成本得投资策略。三、 条件假设 除购入价折旧以及运营与维护成本外无其她费用;四、模型建立 二 5 11 7 三 6 4 1 6 6 1 3 8 四 一 9 12 8 11 20 五 1 0 六运用 Diji kst ra 算法 1 2 3 4 5 60 4 6 9 12 2 0 6 9 12 20 9 12 2 0 12 20 20可...