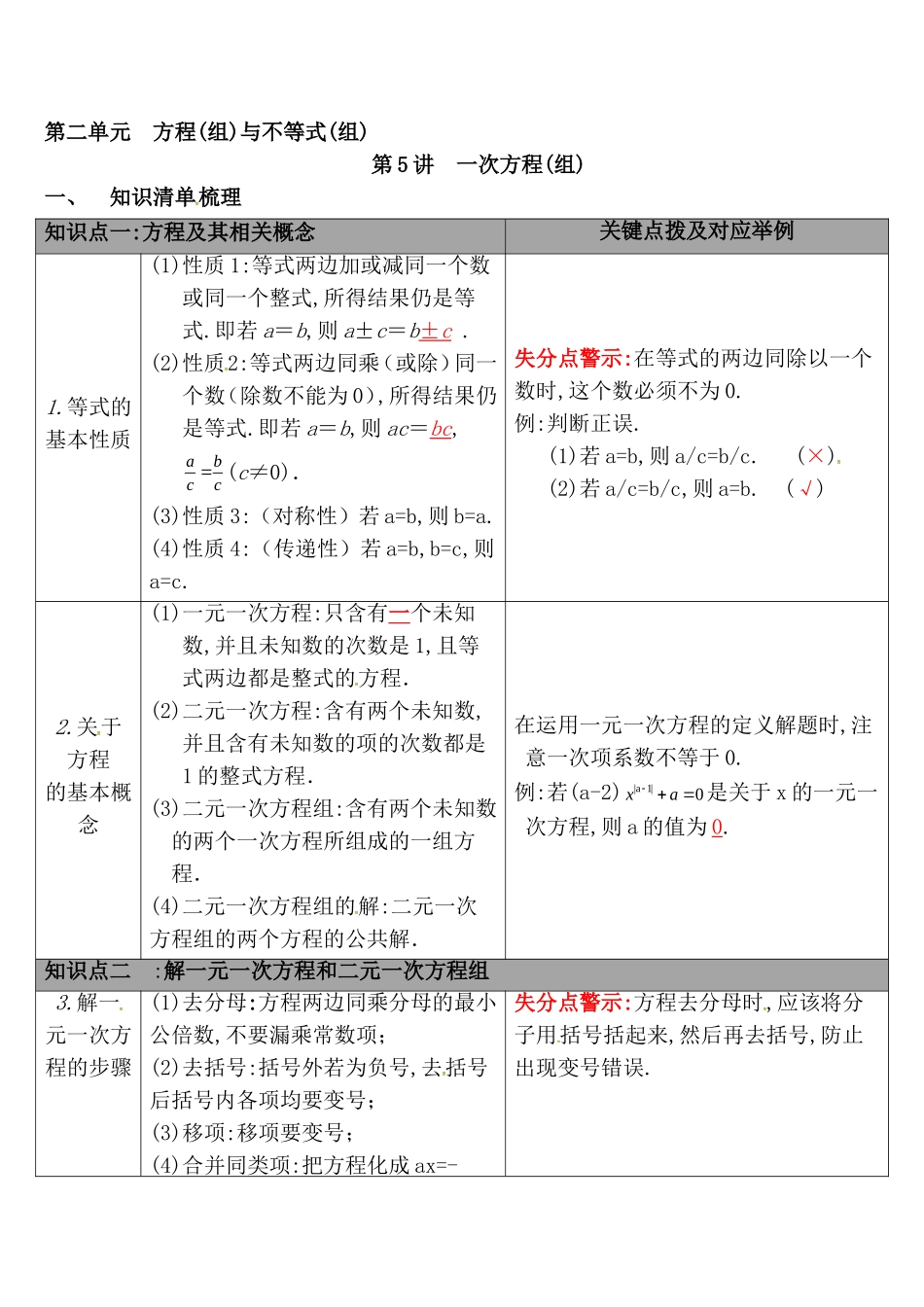
【通用版】2019 年中考数学总复习:知识点全梳理第二单元 方程(组)与不等式(组)第 5 讲 一次方程(组)一、知识清单梳理知识点一:方程及其相关概念 关键点拨及对应举例1.等式的基本性质(1)性质 1:等式两边加或减同一个数或同一个整式,所得结果仍是等式.即若 a=b,则 a±c=b± c .(2)性质2:等式两边同乘(或除)同一个数(除数不能为 0),所得结果仍是等式.即若 a=b,则 ac=bc,abcc (c≠0).(3)性质 3:(对称性)若 a=b,则 b=a.(4)性质 4:(传递性)若 a=b,b=c,则a=c.失分点警示:在等式的两边同除以一个数时,这个数必须不为 0.例:判断正误.(1)若 a=b,则 a/c=b/c. (×)(2)若 a/c=b/c,则 a=b. (√)2.关于方程 的基本概念(1)一元一次方程:只含有一个未知数,并且未知数的次数是 1,且等式两边都是整式的方程.(2)二元一次方程:含有两个未知数,并且含有未知数的项的次数都是1 的整式方程.(3)二元一次方程组:含有两个未知数的两个一次方程所组成的一组方程.](4)二元一次方程组的解:二元一次方程组的两个方程的公共解.在运用一元一次方程的定义解题时,注意一次项系数不等于 0.例:若(a-2)|a 1|0xa 是关于 x 的一元一次方程,则 a 的值为 0.知识点二 :解一元一次方程和二元一次方程组3.解一元一次方程的步骤(1)去分母:方程两边同乘分母的最小公倍数,不要漏乘常数项;(2)去括号:括号外若为负号,去括号后括号内各项均要变号;(3)移项:移项要变号;(4)合并同类项:把方程化成 ax=-失分点警示:方程去分母时,应该将分子用括号括起来,然后再去括号,防止出现变号错误.【通用版】2019 年中考数学总复习:知识点全梳理b(a≠0);(5)系数化为 1:方程两边同除以系数a,得到方程的解 x=-b/a.4.二元一次 方程组的解法思路:消元,将二元一次方程转化为一元一次方程.已知方程组,求相关代数式的值时,需注意观察,有时不需解出方程组,利用整体思想解决解方程组. 例: 已知2923xyxy 则 x-y 的值为 x-y=4.方法:(1)代入消元法:从一个方程中求出某一个未知数的表达式,再把“它”代入另一个方程,进行求解;(2) 加减消元法:把两个方程的两边分别相加或相减消去一个未知数的方法.知识点三 :一次方程(组)的实际应用5.列方程(组) 解应用题的一般步骤(1)审题:审清题意,分清题中的已知量、未知量;(2)设未知数;(3)列方程(组):找出等量关系,列方程(组);(4)解方程(组);(5)检验:检验所解答案是否正确或是否满...