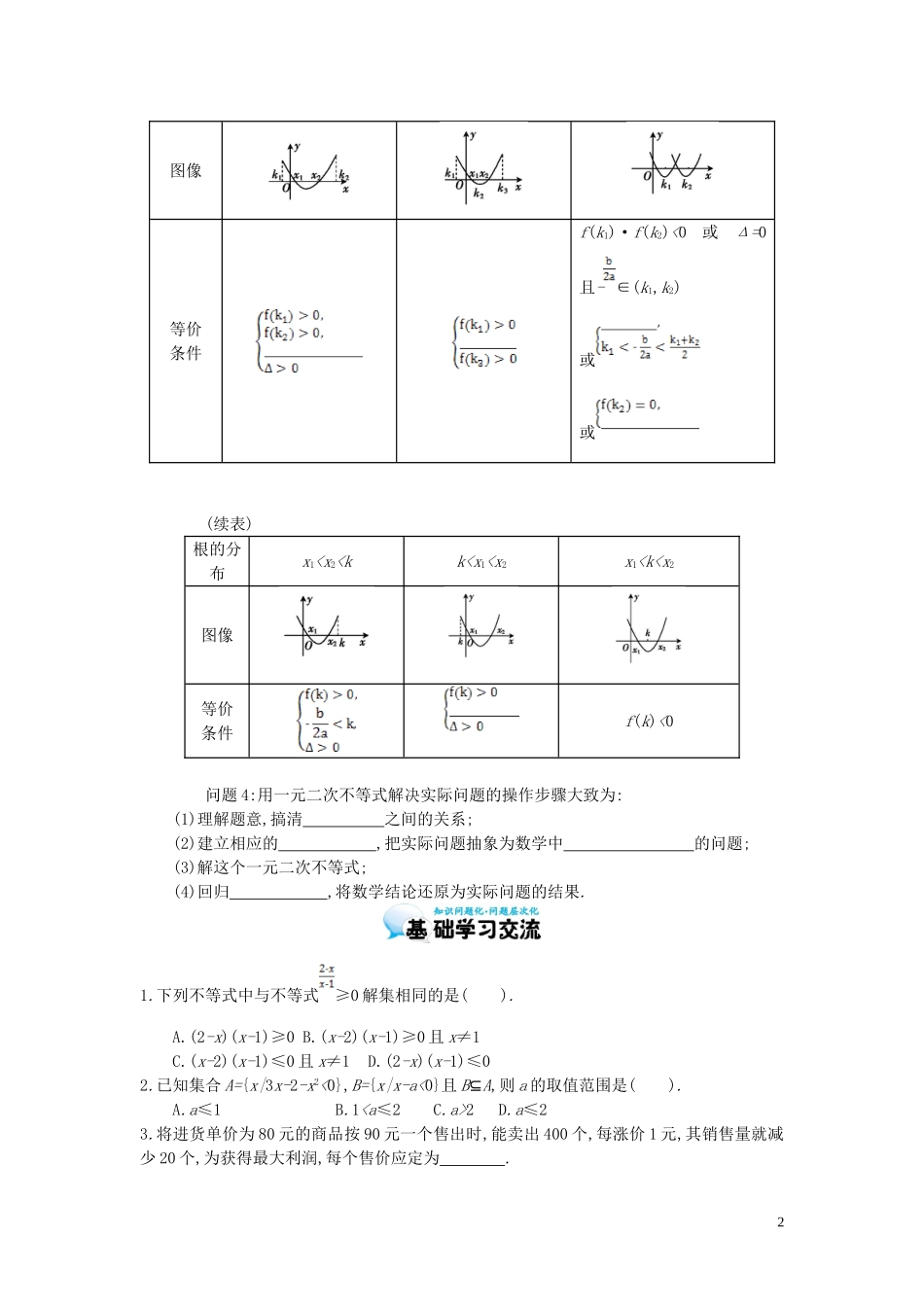
第 4 课时 一元二次不等式及其解法的应用1.熟悉简单的一元高次不等式和分式不等式的解法.2.理解一元二次方程根的分布问题.3.会用一元二次不等式解决实际问题.上一课时我们共同学习了一元二次不等式的解法,并能解简单的一元二次不等式,一元二次不等式及其解法是一种重要的数学工具,是集合、函数、不等式等知识的综合交汇点,地位重要,这一讲我们将共同探究一元二次不等式及其解法的应用.问题 1:简单的一元高次不等式和分式不等式的解法一元高次不等式 f(x)>0 用 (或称数轴穿根法,根轴法,区间法)求解,其步骤是: (1)将 f(x)最高次项的系数化为 数; (2)将 f(x)分解为若干个一次因式的积或者若干个 之积; (3)将每一个一次因式的根标在数轴上,从 依次穿过每一点画曲线(注意重根情况,偶次方根穿而不过,奇次方根既穿又过); (4)根据曲线显现出的 f(x)值的符号变化规律,写出 . 由上归纳出重要步骤:① 化标(化成标准形式);② 找根;③ 标根;④ 串根(奇透偶不透).问题 2:分式不等式:先整理成标准型>0(<0)或≥0(≤0),再化成整式不等式来解.(1)>0⇔f(x)·g(x)>0.(2)<0⇔f(x)·g(x)<0.(3)≥0⇔(4)≤0⇔问题 3:一元二次方程 ax2+bx+c=0(a>0)的根的分布问题:记 f(x)=ax2+bx+c,其根的情况、图像情况、不等式的三者关系如下:根的分布k1
2D.a≤23.将进货单价为 80 元的商品按 90 元一个售出时,能卖出 400 个,每涨价 1 元,其销售量就减少 20 个,为获得最大利润,每个售价应定为 . 24.不等式<0 的解集为 R,求实数 m 的取值范围.简单的高次不等式解法解不等式:(x-1)(3-x)(x+ )<0.分式不等式的解法解下列分式不等式:(1)≥0;(2)>1(a≠1 且 a 为常数).一元二次不等式的实际应用一个服装厂生产风衣,月销售量 x(件...