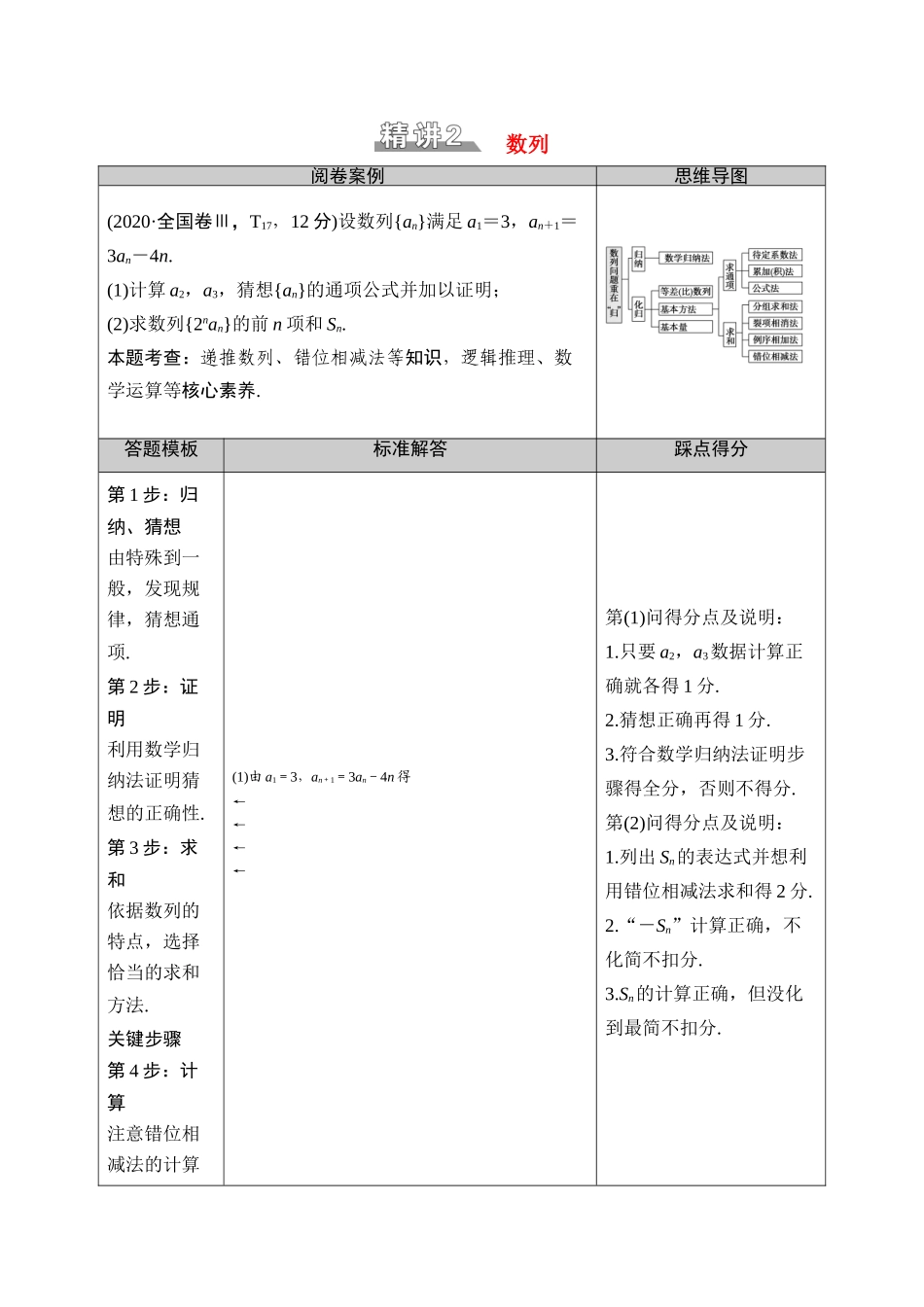
数列阅卷案例思维导图(2020·全国卷Ⅲ,T17,12 分)设数列{an}满足 a1=3,an+1=3an-4n.(1)计算 a2,a3,猜想{an}的通项公式并加以证明;(2)求数列{2nan}的前 n 项和 Sn.本题考查:递推数列、错位相减法等知识,逻辑推理、数学运算等核心素养.答题模板标准解答踩点得分第 1 步:归纳、猜想由特殊到一般,发现规律,猜想通项.第 2 步:证明利用数学归纳法证明猜想的正确性.第 3 步:求和依据数列的特点,选择恰当的求和方法.关键步骤第 4 步:计算注意错位相减法的计算(1)由 a1=3,an+1=3an-4n 得←←←←第(1)问得分点及说明: 1.只要 a2,a3数据计算正确就各得 1 分.2.猜想正确再得 1 分.3.符合数学归纳法证明步骤得全分,否则不得分.第(2)问得分点及说明:1.列出 Sn的表达式并想利用错位相减法求和得 2 分.2.“-Sn”计算正确,不化简不扣分.3.Sn的计算正确,但没化到最简不扣分.方法,计算务必细心.命题点 1 等差、等比数列的基本量的运算 1.两组重要公式(1)等差数列:① Sn==na1+d;②am=an+(m-n)d;③ 若 m,n,p 成等差数列,则 2an=am+ap.(2)等比数列:① Sn==(q≠1);②am=an·qm-n;③ 若 m,n,p 成等比数列,则 a=am·ap.2.等差(比)数列的运算技巧:(1)在进行等差(比)数列项与和的运算时,若条件和结论间的联系不明显,则均可化成关于 a1和 d(q)的方程组求解;(2)要注意消元法及整体计算,以减少计算量.3.由等差数列、等比数列组成的综合问题,首先要根据两数列的概念,设出相应的基本量,充分使用通项公式、求和公式、数列的性质,确定基本量.解综合题的成败在于审清题目,弄懂来龙去脉,揭示问题的内在联系和隐含条件,形成解题策略. [高考题型全通关]1.(2020·全国卷Ⅲ)设等比数列{an}满足 a1+a2=4,a3-a1=8.(1)求{an}的通项公式;(2)记 Sn为数列{log3an}的前 n 项和.若 Sm+Sm+1=Sm+3,求 m.[解] (1)设{an}的公比为 q,则 an=a1qn-1.由已知得解得 a1=1,q=3.所以{an}的通项公式为 an=3n-1.(2)由(1)知 log3an=n-1.故 Sn=.由 Sm+Sm+1=Sm+3得 m(m-1)+(m+1)m=(m+3)(m+2),即 m2-5m-6=0.解得 m=-1(舍去),m=6.2.(2020·惠州第二次调研)在数列{an}中,a1=1,a2=,an+1=an+,其中n∈N*,λ 为常数.(1)求 λ 的值;(2)设 bn=,求数列{bn}的通项公式.[解] (1)将 n=1 代入 an+1=an+,得 a2=2...