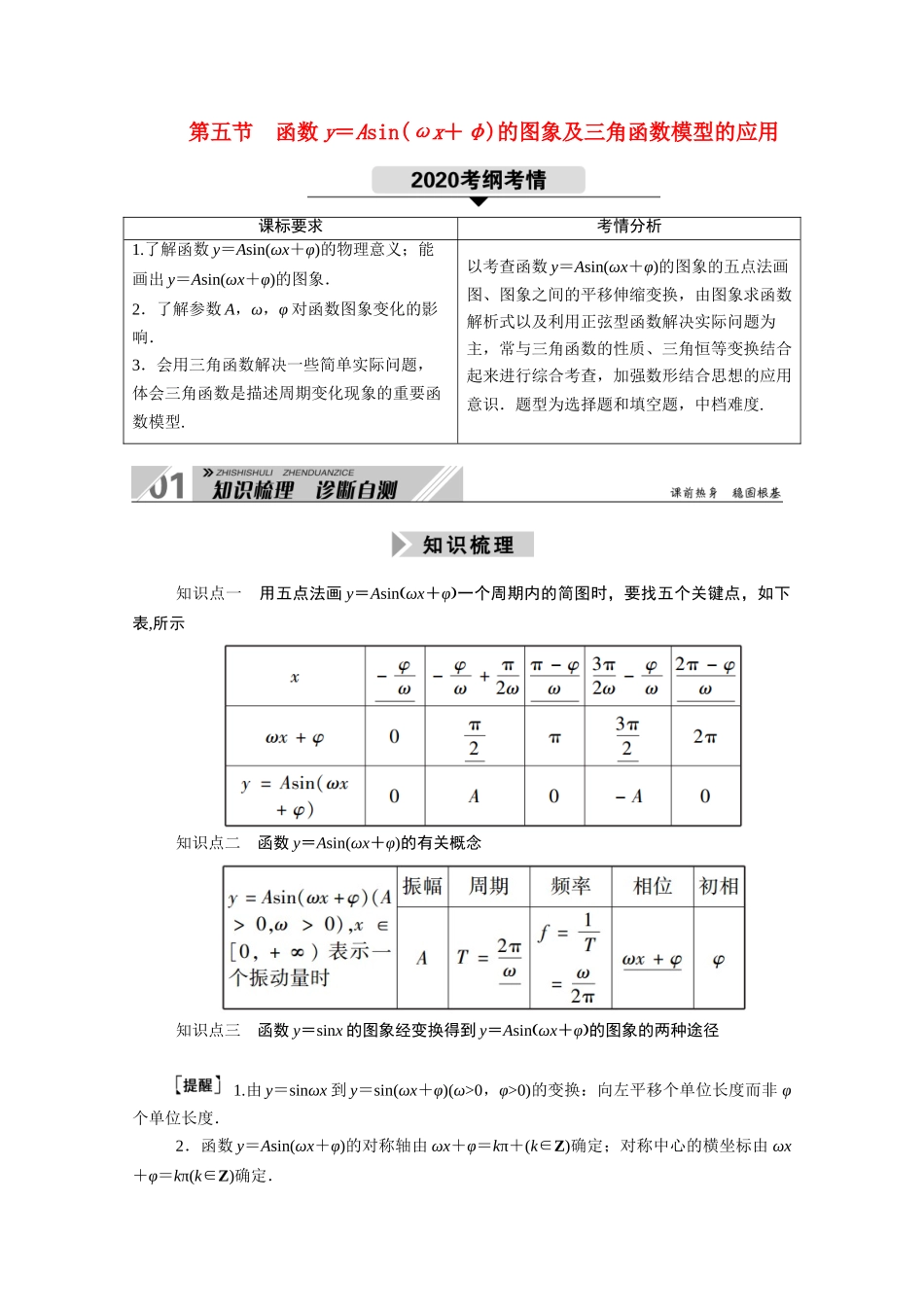
第五节 函数 y=Asin(ωx+φ)的图象及三角函数模型的应用课标要求考情分析1.了解函数 y=Asin(ωx+φ)的物理意义;能画出 y=Asin(ωx+φ)的图象.2.了解参数 A,ω,φ 对函数图象变化的影响.3.会用三角函数解决一些简单实际问题,体会三角函数是描述周期变化现象的重要函数模型.以考查函数 y=Asin(ωx+φ)的图象的五点法画图、图象之间的平移伸缩变换,由图象求函数解析式以及利用正弦型函数解决实际问题为主,常与三角函数的性质、三角恒等变换结合起来进行综合考查,加强数形结合思想的应用意识.题型为选择题和填空题,中档难度. 知识点一 用五点法画 y=Asinωx+φ一个周期内的简图时,要找五个关键点,如下表,所示知识点二 函数 y=Asin(ωx+φ)的有关概念知识点三 函数 y=sinx 的图象经变换得到 y=Asinωx+φ的图象的两种途径1.由 y=sinωx 到 y=sin(ωx+φ)(ω>0,φ>0)的变换:向左平移个单位长度而非 φ个单位长度.2.函数 y=Asin(ωx+φ)的对称轴由 ωx+φ=kπ+(k∈Z)确定;对称中心的横坐标由 ωx+φ=kπ(k∈Z)确定.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)将函数 y=3sin2x 的图象左移个单位长度后所得图象的解析式是 y=3sin.( × )(2)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( × )(3)函数 y=Acos(ωx+φ)的最小正周期为 T,那么函数图象的两个相邻对称中心之间的距离为.( √ )解析:根据 y=Asin(ωx+φ)的图象与性质知(1)(2)是错误的,(3)是正确的.2.小题热身(1)函数 y=2sin 的振幅、频率和初相分别为( A )A.2,, B.2,,C.2,, D.2,,-(2)为了得到函数 y=2sin 的图象,可以将函数 y=2sin2x 的图象( A )A.向右平移个单位长度 B.向右平移个单位长度C.向左平移个单位长度 D.向左平移个单位长度(3)用五点法作函数 y=sin 在一个周期内的图象时,主要确定的五个点是、、、、.(4)函数 y=Asin(ωx+φ)(A,ω,φ 为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图所示,则 ω=3.(5)将函数 y=2sin 的图象向右平移个周期后,所得图象对应的函数解析式为 y = 2sin .解析:(1)由振幅、频率和初相的定义可知,函数 y=2sin 的振幅为 2,频率为,初相为.(2)函数 y=2sin=2sin,可由函数 y=2sin2x 的图象向右平移个单位长度得到.(5)函数 y=2sin ...