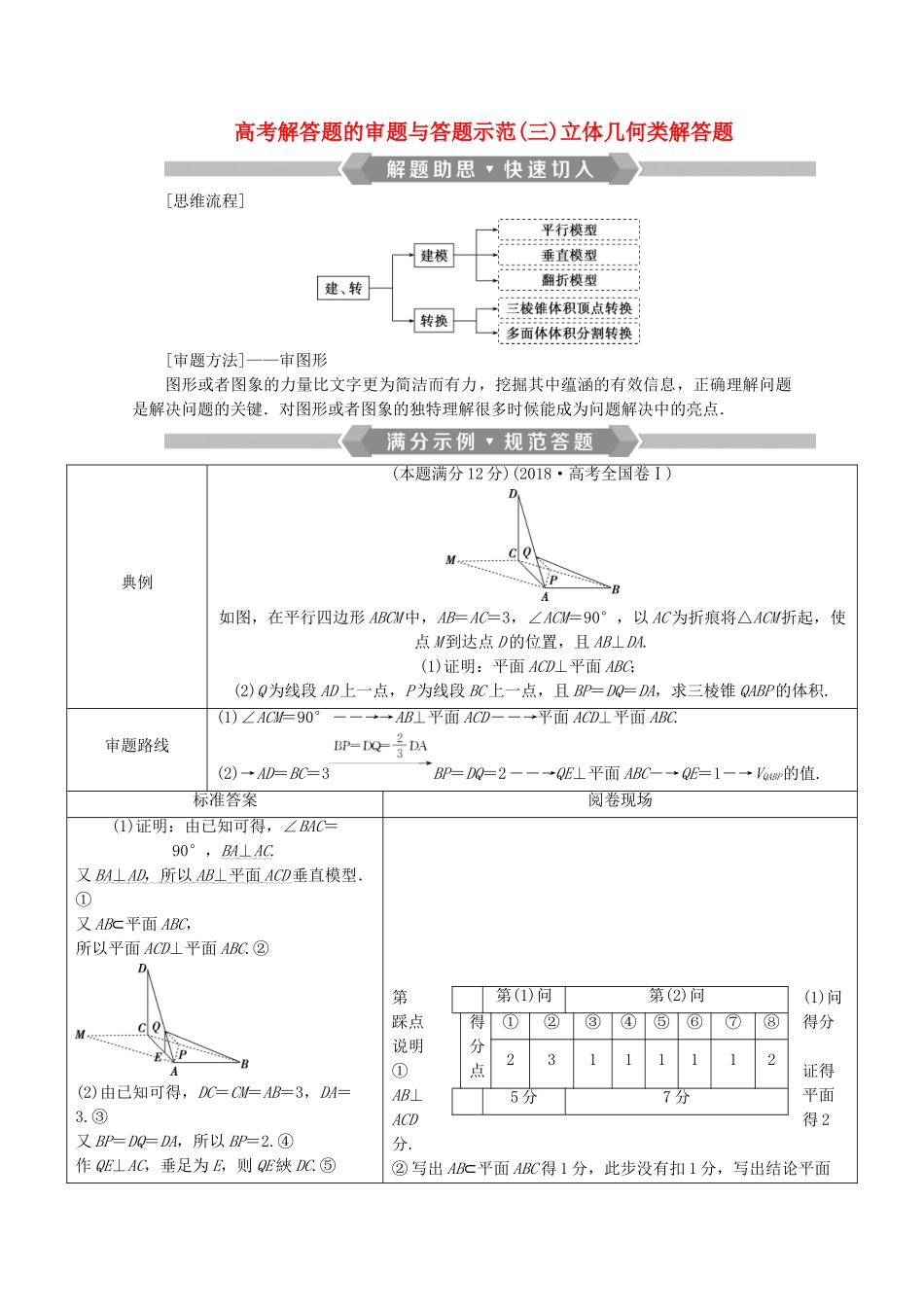
高考解答题的审题与答题示范(三)立体几何类解答题[思维流程][审题方法]——审图形图形或者图象的力量比文字更为简洁而有力,挖掘其中蕴涵的有效信息,正确理解问题是解决问题的关键.对图形或者图象的独特理解很多时候能成为问题解决中的亮点.典例(本题满分 12 分)(2018·高考全国卷Ⅰ)如图,在平行四边形 ABCM 中,AB=AC=3,∠ACM=90°,以 AC 为折痕将△ACM 折起,使点 M 到达点 D 的位置,且 AB⊥DA.(1)证明:平面 ACD⊥平面 ABC;(2)Q 为线段 AD 上一点,P 为线段 BC 上一点,且 BP=DQ=DA,求三棱锥 QABP 的体积.审题路线(1)∠ACM=90°――→→AB⊥平面 ACD――→平面 ACD⊥平面 ABC.(2)→AD=BC=3BP=DQ=2――→QE⊥平面 ABC―→QE=1―→VQABP的值.标准答案阅卷现场(1)证明:由已知可得,∠BAC=90°,BA ⊥ AC .又 BA ⊥ AD , 所以 AB ⊥ 平面 ACD 垂直模型.①又 AB⊂平面 ABC,所以平面 ACD⊥平面 ABC.②(2)由已知可得,DC=CM=AB=3,DA=3.③又 BP=DQ=DA,所以 BP=2.④作 QE⊥AC,垂足为 E,则 QE 綊 DC.⑤第(1)问踩点得分说明①证得AB⊥平面ACD得 2分.② 写出 AB⊂平面 ABC 得 1 分,此步没有扣 1 分,写出结论平面第(1)问第(2)问得分点①②③④⑤⑥⑦⑧231111125 分7 分由已知及(1)可得 DC⊥平面 ABC,⑥所以 QE⊥平面 ABC,QE=1.⑦因此,三棱锥 QABP 的体积为VQABP=×QE×S△ABP=×1××3×2sin 45°=1.⑧ABC⊥平面 ACD 得 2 分.第(2)问踩点得分说明③ 写出 AD=3 或 BC=3 得 1 分.④ 计算出 BP=2 或 AQ=得 1 分.⑤ 作 QE⊥AC 得 1 分.⑥ 由面面垂直的性质推出 DC⊥平面 ABC 得 1 分.⑦ 写出 QE=1 得 1 分.⑧ 正确计算出 VQABP=1 得 2 分.