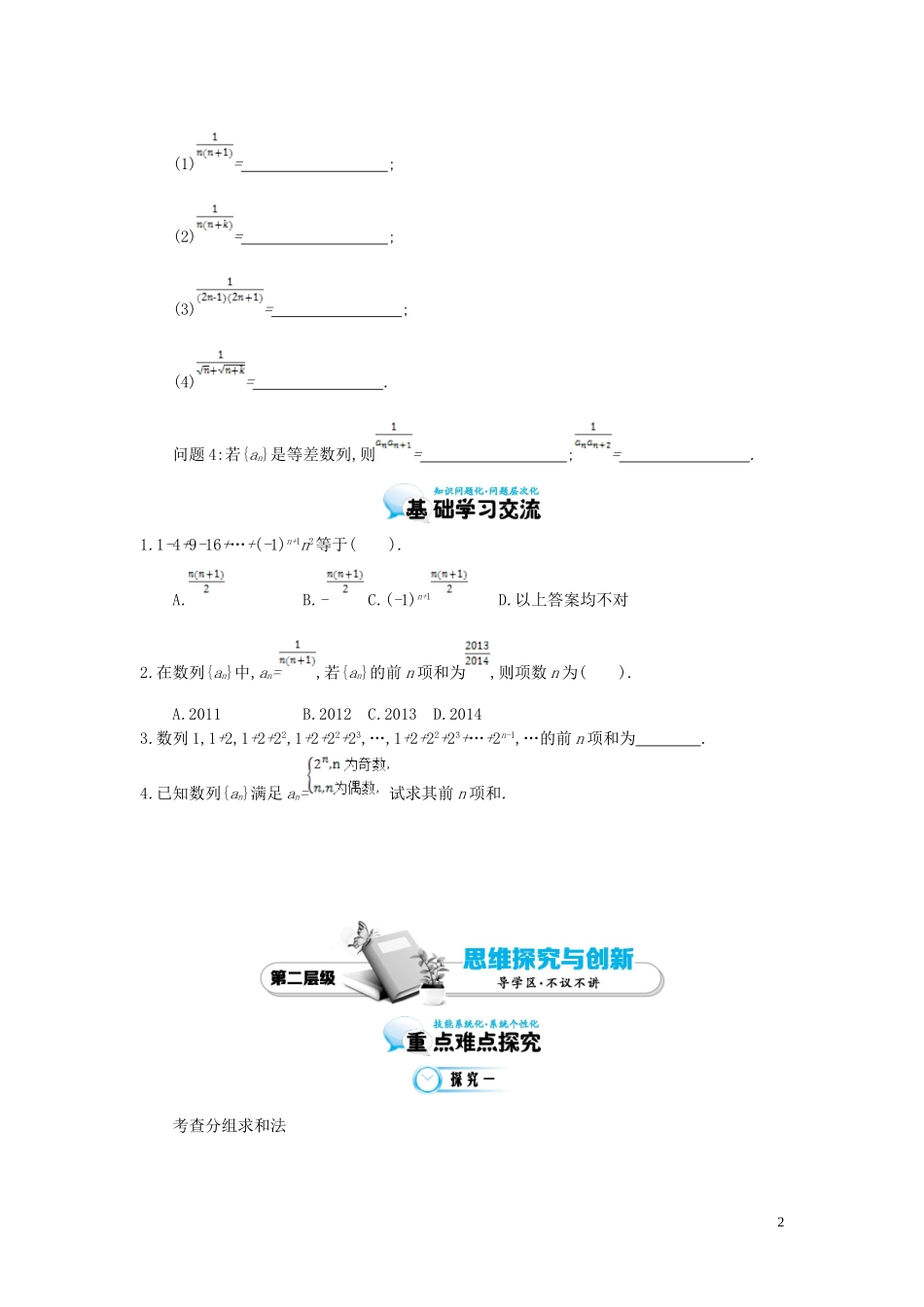
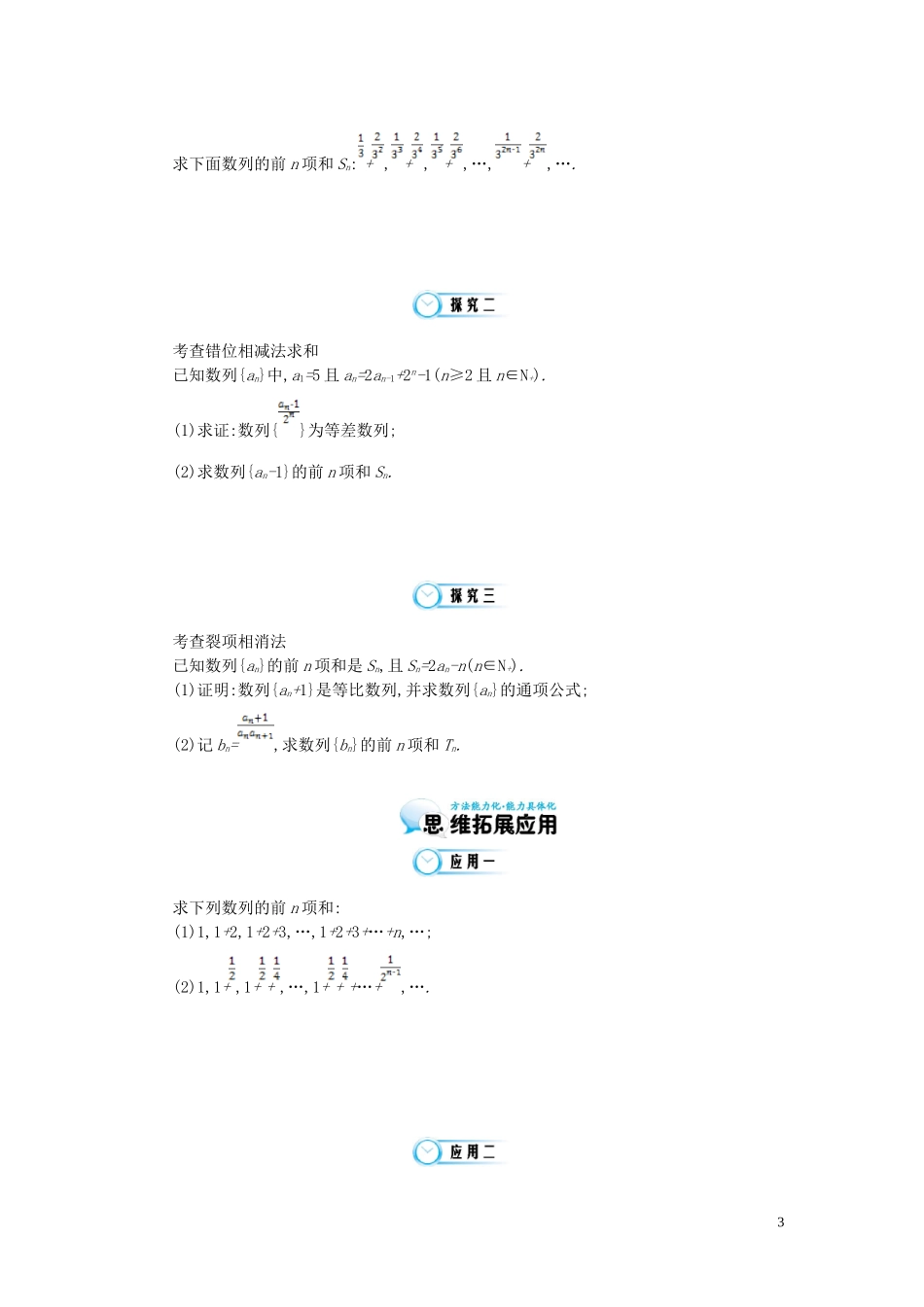
第 10 课时 前 n 项和 Sn的求法1.理解等差数列、等比数列的求和公式.2.掌握公式法、倒序相加法、错位相减法、裂项相消法等方法.3.初步利用各种求和方法解决有关数列求和问题.在推导等差数列的前 n 项和公式的时候我们用了倒序相加法,在推导等比数列的前 n 项和公式的时候我们用了错位相减法,今天,我们一起来看看数列的前 n 项和有哪些求法?问题 1:公式法:(1)如果一个数列是等差数列或等比数列,则求和时直接利用等差、等比数列的前 n 项和公式,注意等比数列公比 q 的取值情况要分 . (2)一些常见数列的前 n 项和公式:①1+2+3+4+…+n= ; ②1+3+5+7+…+2n-1= ; ③2+4+6+8+…+2n= ; ④12+22+32+…+n2= n(n+1)(2n+1);⑤13+23+33+…+n3= n2(n+1)2;⑥1×2+2×3+…+n×(n+1)=.问题 2:(1)倒序相加法:如果一个数列{an},首末两端等“距离”的两项的和相等或等于同一常数,那么求这个数列的前 n 项和即可用倒序相加法.(2)分组求和法:若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转化法,分别求和而后相加减.(3)错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前 n 项和即可用此法来求,等比数列的前 n 项和就是用此法推导的.(4)裂项相消法:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.问题 3:常见的拆项公式有:1(1)= ; (2)= ; (3)= ; (4)= . 问题 4:若{an}是等差数列,则= ;= . 1.1-4+9-16+…+(-1)n+1n2等于( ).A. B.-C.(-1)n+1D.以上答案均不对2.在数列{an}中,an=,若{an}的前 n 项和为,则项数 n 为( ).A.2011 B.2012C.2013D.20143.数列 1,1+2,1+2+22,1+2+22+23,…,1+2+22+23+…+2n-1,…的前 n 项和为 . 4.已知数列{an}满足 an=试求其前 n 项和.考查分组求和法2求下面数列的前 n 项和 Sn: + , + , + ,…,+,….考查错位相减法求和已知数列{an}中,a1=5 且 an=2an-1+2n-1(n≥2 且 n∈N+).(1)求证:数列{}为等差数列;(2)求数列{an-1}的前 n 项和 Sn.考查裂项相消法已知数列{an}的前 n 项和是 Sn,且 Sn=2an-n(n∈N+).(1)证明:数列{an+1}是等比数列,并求数列{an}的通项公式;(2)记 bn=,求数列{bn}的前 n 项和 Tn. 求下列数列的前 n 项和:(1)1,1+2,1+2+3,…,1+2+3+…+n,…;(2)1,1+ ,1+ + ,…,1+ + +…+,….3已知数列{an}满足:a1=2,an+1=3an+3n+1-...