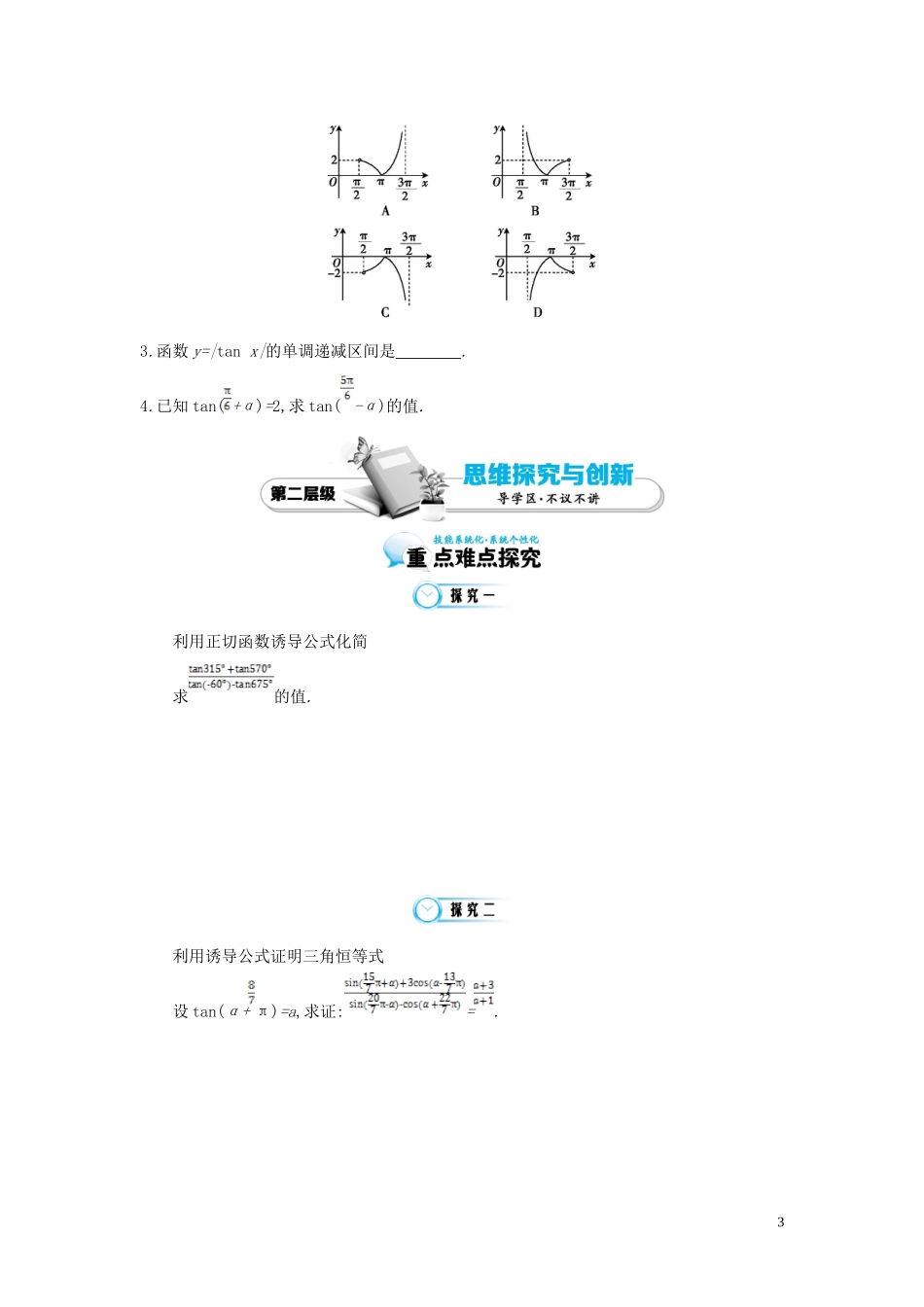
第 8 课时 正切函数的诱导公式1.用类比的方法学习、熟记正切函数的诱导公式. 2.了解正切函数诱导公式的特点,能利用正切函数诱导公式解决简单的问题.前面我们学习了正弦函数、余弦函数的诱导公式,知道角 α 与形如 k· ±α(k∈Z)的正弦、余弦函数值的关系,那么角 α 的正切函数值是否也有相应的关系式呢?今天我们就来探讨一下这个问题.问题 1:下列各角的终边与角 α 的终边的关系角2kπ+α(k∈Z)π+α-α图示与角 α 终边的关系 角π-α-α+α图示与角 α 终边的关系 问题 2:请根据点的对称性推导“-α,π+α,π-α”的诱导公式.设角 α 与单位圆的交点为(a,b),(1)-α 与 α 的终边与单位圆的交点关于 x 轴对称,-α 与单位圆的交点为(a,-b).sin(-α)=-sin α,cos(-α)=cos α,tan(-α)= . (2)α+π 与 α 的终边与单位圆的交点关于原点对称,α+π 与单位圆的交点为(-a,-1b).sin(α+π)=-sin α,cos(α+π)=-cos α,tan(π+α)= . (3)π-α 与 α 的终边与单位圆的交点关于 y 轴对称,π-α 与单位圆的交点为(-a,b),sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)= . 问题 3:形如“ -α, +α”的诱导公式的推导设角 α 与单位圆的交点为(a,b),(1) -α 的终边与 x 的终边关于 y=x 对称,与单位圆交点坐标称为(b,a),sin( -α)=cos α,cos( -α)=sin α,tan( -α)= . (2) +α 的终边即 α 的终边逆时针旋转 90°,与单位圆交点坐标为(-b,a),sin(+α)=cos α,cos( +α)=-sin α,tan( +α)= . 问题 4:正切函数的诱导公式有哪些?(1)tan(α+kπ)= ,其中 k∈Z. (2)tan(-α)= . (3)tan(π-α)= . (4)tan(π+α)= . (5)tan(2π-α)= . (6)tan( +α)= . (7)tan( -α)= . 1.已知 cot( -α)= ,则 tan(α- )的值是( ).A.- B. C.- D.2.函数 y=tan x+sin x-|tan x-sin x|在区间( , )内的图像大致是( ).23.函数 y=|tan x|的单调递减区间是 . 4.已知 tan( +α)=2,求 tan( -α)的值.利用正切函数诱导公式化简求的值.利用诱导公式证明三角恒等式设 tan(α+ π)=a,求证:=.3利用正切函数诱导公式求值已知角 α 终边上的一点 A(,-1),求的值.化简:.求证:=-tan α.已知 α 为第四象限角,且 tan α 是方程 x2-x-12=0 的一个根,求的值.41.下列不等式中,正确的是( ).A.tan >tanB.tan tan(-)2.化简的...