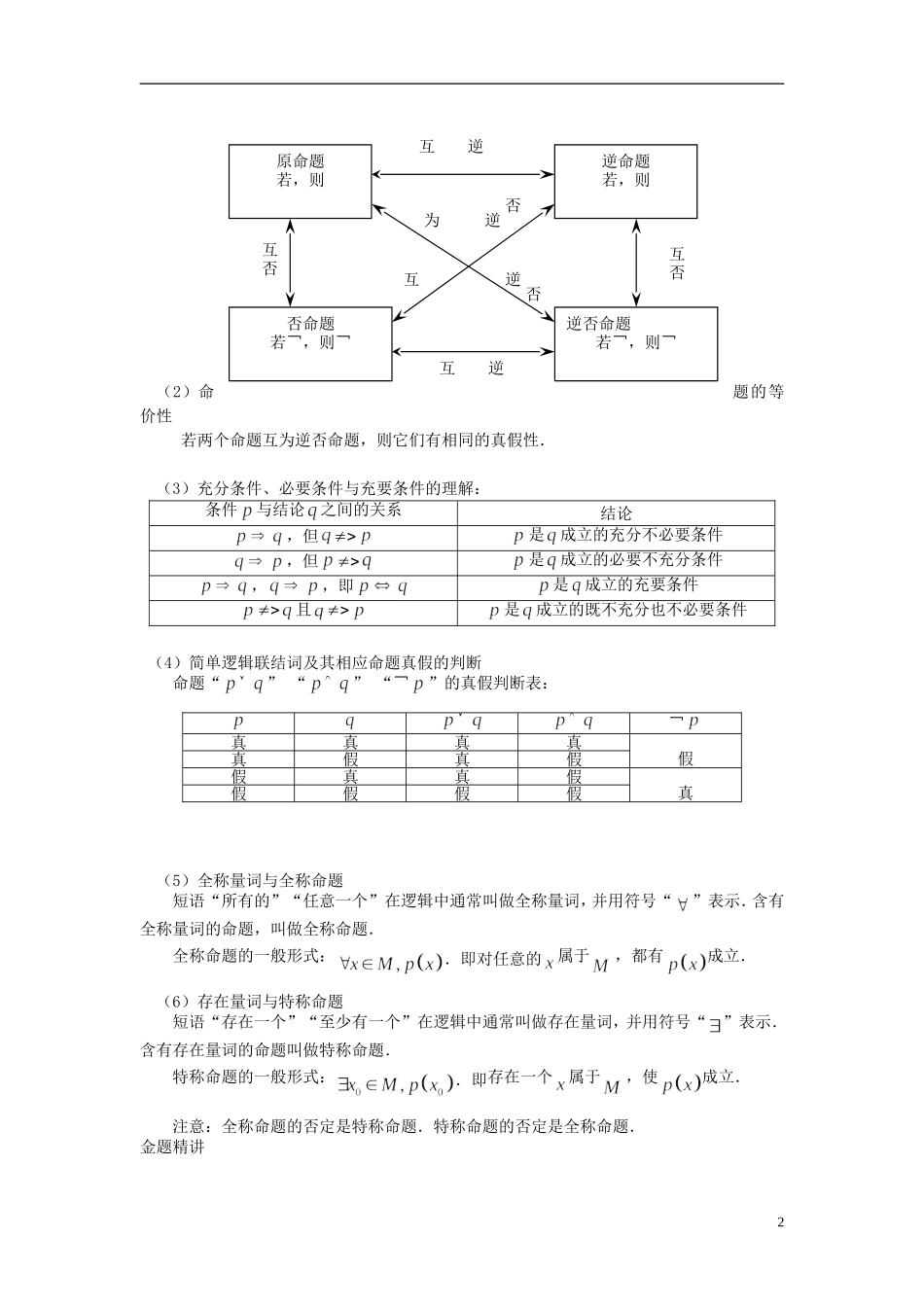
集合与常用逻辑用语经典回顾开篇语集合与常用逻辑用语是高中数学的基础内容之一在高考中大多以选择题或填空题的形式出现,着重考查元素与集合、集合与集合的关系,集合的运算,四种命题及其关系,充分条件与必要条件,简单逻辑联结词,全称量词语和存在量词.本节课我们将列举几个集合与常用逻辑用语的经典问题,并介绍它们的求解方法.开心自测题一:若集合,,则( ).(A) (B) (C) (D) 题二:命题“存在R,0”的否定是( ).(A)不存在R,>0 (B)存在R,0 (C)对任意的R, 0 (D)对任意的R,>0考点梳理1.集合(1)子集和真子集① 子集:集合的任何一个元素都是集合的元素,则称是的子集(或包含),记作.② 真子集:若且,则称是的真子集,记作.③ 两个集合相等:若,且,则称等于,记作.(2) 集合的运算:① 交集:由所有属于集合,且属于集合的元素组成的集合叫做集合与的交集,记作,即.② 并集:由所有属于集合,或属于集合的元素组成的集合叫做集合与的并集,记作,即.③ 全集:包含了所要研究的各个集合的全部元素的集合称为全集,记作. ④ 补集:若是一个集合,,则由中不属于集合的元素构成的集合中子集的补集,记作.2.常用逻辑用语(1)四种命题及其相互之间的关系1(2)命题的等价性若两个命题互为逆否命题,则它们有相同的真假性.(3)充分条件、必要条件与充要条件的理解:条件与结论之间的关系结论,但是成立的充分不必要条件,但是成立的必要不充分条件,,即是成立的充要条件且是成立的既不充分也不必要条件(4)简单逻辑联结词及其相应命题真假的判断命题“” “” “¬”的真假判断表:(5)全称量词与全称命题短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“”表示.含有全称量词的命题,叫做全称命题.全称命题的一般形式:.即对任意的属于,都有成立.(6)存在量词与特称命题短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“”表示.含有存在量词的命题叫做特称命题.特称命题的一般形式:.即存在一个属于,使成立.注意:全称命题的否定是特称命题.特称命题的否定是全称命题.金题精讲¬真真真真假真假真假假真真假真假假假假2逆互否 互 逆原命题若,则逆命题若,则否命题若¬,则¬逆否命题若¬,则¬ 互 逆互否互为逆否否题一:若{Un n是小于 9 的正整数},{AnU n是奇数},{BnU n是 3 的倍数...