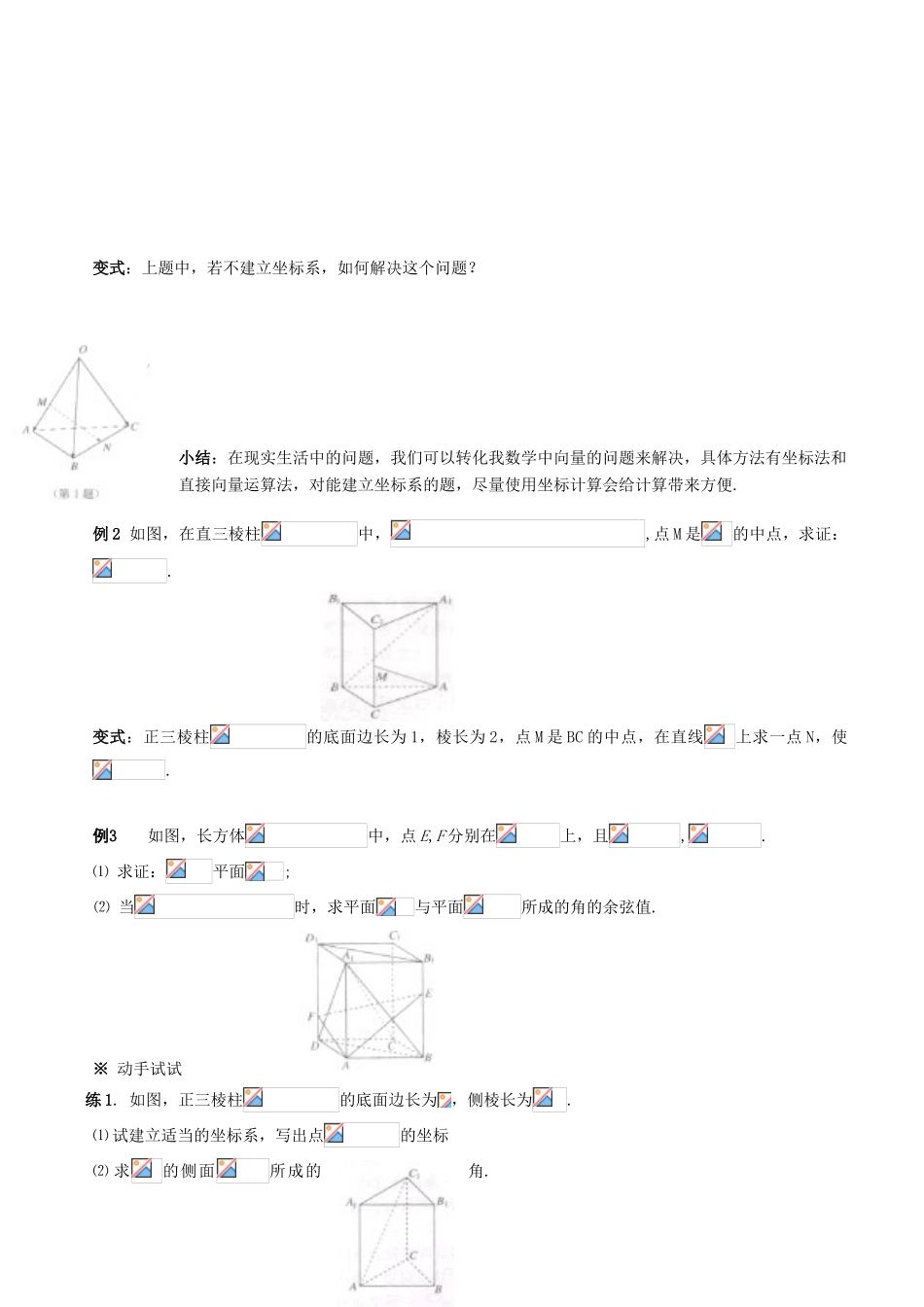
§第三章 空间向量（复习） 学习目标 1
掌握空间向量的运算及其坐标运算；2
立体几何问题的解决──熟练掌握向量是很好的工具
学习过程 一、课前准备（预习教材 P115－116，找出惑之处）复习 1：如图，空间四边形中，
点 M 在 OA 上，且 OM=2MA, N 为 BC 中点，则 复习 2：平行六面体中，，点 P,M,N 分别是的中点，点 Q 在上，且,用基底表示下列向量：⑴ ; ⑵ ; ⑶ ; ⑷
※主要知识点：1
空间向量的运算及其坐标运算：空间向量是平面向量的推广, 有关运算方法几乎一样,只是“二维的”变成 “三维的”了
立体几何问题的解决──向量是很好的工具① 平行与垂直的判断 ②角与距离的计算※ 典型例题例 1 如图,一块均匀的正三角形面的钢板的质量为，在它的顶点处分别受 力、、， 每 个力与同它相邻的三角形的两边之间的夹角都是，且
这块钢板在这些力的作用下将会怎样运动
这三个力最小为多大时，才能提起这块钢板
变式：上题中，若不建立坐标系，如何解决这个问题
小结：在现实生活中的问题，我们可以转化我数学中向量的问题来解决，具体方法有坐标法和直接向量运算法，对能建立坐标系的题，尽量使用坐标计算会给计算带来方便
例 2 如图，在直三棱柱中，,点 M 是的中点，求证：
变式：正三棱柱的底面边长为 1，棱长为 2，点 M 是 BC 的中点，在直线上求一点 N，使
例3 如图，长方体中，点 E,F 分别在上，且,
⑴ 求证：平面;⑵ 当时，求平面与平面所成的角的余弦值
※ 动手试试练 1
如图，正三棱柱的底面边长为，侧棱长为
⑴ 试建立适当的坐标系，写出点的坐标⑵ 求的侧面所成的角
已知点 A(1,-2,0),向量，求点 B 的坐标，使得，且
三、总结提升※ 学习小结1
空间向量的运算与平面向量的方法相同；2
向量的数量积和平面的法向
