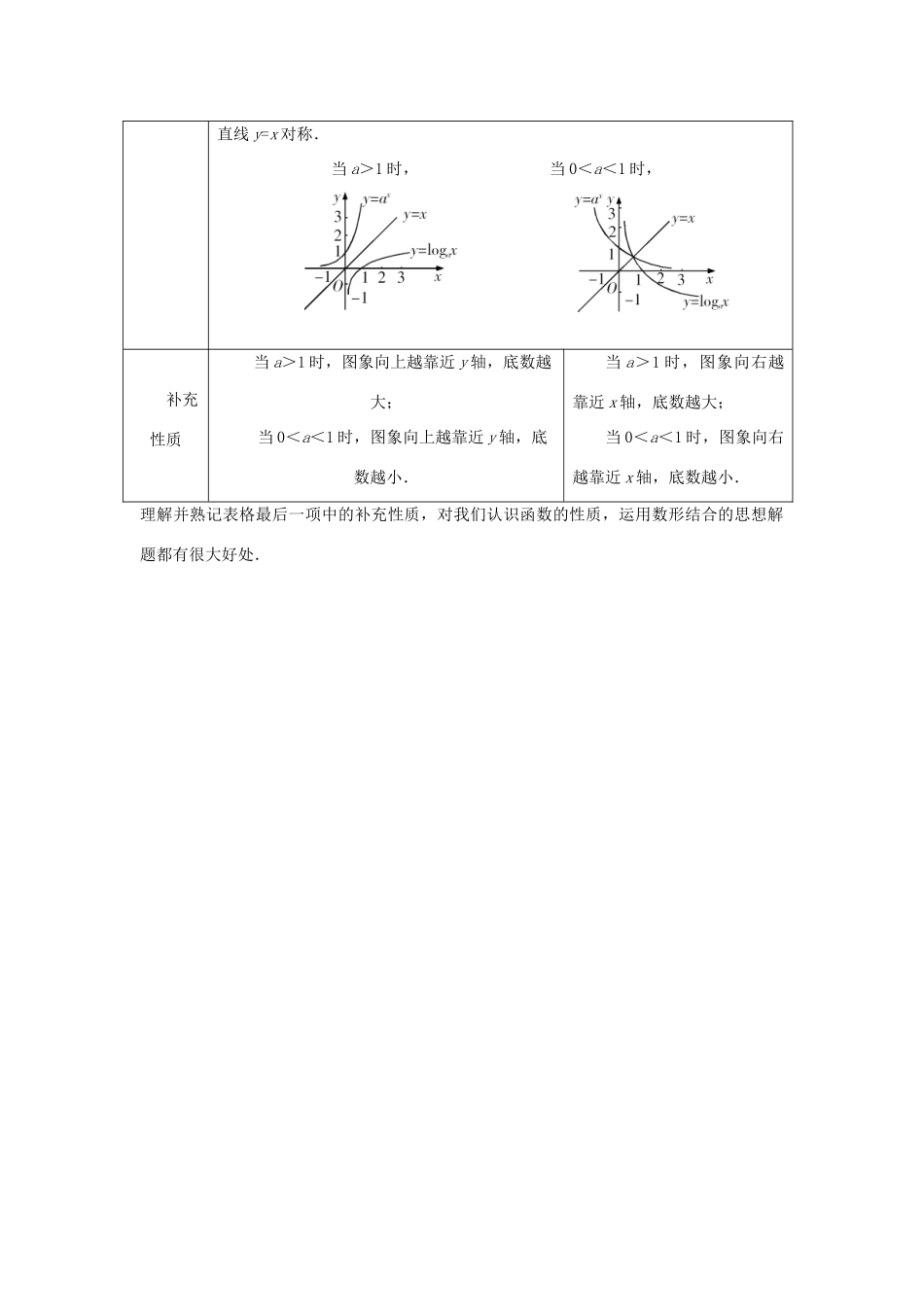
指数函数与对数函数对照表前面我们刚学了指数函数,现在我们又学了对数函数,而且同底的指数函数和对数函数互为反函数,你能分清它们之间的区别与联系吗?下表可帮助同学们理顺它们之间的关系,以形成对它们的整体认识.指数函数和对数函数对照表名称指数函数对数函数一般形式定义域R(0,+∞)值域(0,+∞)R函数值变化情况当时,当时,当时,当时,单调性当时,是增函数;当时,是减函数.当时,是增函数;当时,是减函数.图象(a>0 且 a≠1) 的图象与(a>0 且 a≠1)的图象关于直线 y=x 对称.当 a>1 时, 当 0<a<1 时, 补充性质当 a>1 时,图象向上越靠近 y 轴,底数越大;当 0<a<1 时,图象向上越靠近 y 轴,底数越小.当 a>1 时,图象向右越靠近 x 轴,底数越大;当 0<a<1 时,图象向右越靠近 x 轴,底数越小.理解并熟记表格最后一项中的补充性质,对我们认识函数的性质,运用数形结合的思想解题都有很大好处.对数函数创新题两例函数中的创新题,一般会给出新定义、新运算等,这就要求我们读懂题目,并把新概念、新定义、新运算与所学知识相结合,在较高层次上分析问题、解决问题.例 1 定义:函数,x∈D,若存在常数 C,对于任意 x1∈D,存在惟一的 x2∈D,使 得, 则 称 函 数在 D 上 的 “ 均 值 ” 为 C , 已 知=lgx,x∈[10,100],则函数=lgx 在[10,100]上的均值为( ).(A)(B)(C)(D)10解析:由题意,当 10≤x1≤100 时,x2也要在[10,100]内,且,即 x1x2是常数.令,又≤≤, ∴,∴m=1000,∴.点 评 : 本 题 是 新 定 义 题 , 其 关 键 是 在 [ 10 , 100 ] 上 x2 被 x1 惟 一 确 定 , 且为常数,故可令,然后依据 x2∈[10,100],求出 m=1000,再由求出C.例 2 给定,n∈N*,定义使 a1·a2·a3·…·ak为整数的 k(k∈N*)叫做“企盼数”,求区间(1,62)内的所有企盼数的和. 解: ,∴a1·a2·a3·…·ak=log23×log34×log45×…×log(k+1)(k+2)=.设为整数 m,即.∴,即,又 k∈(1,62),即 1<2m-2<62,∴3<2m<64,∴m=2,3,4,5,代入得到 k=2,6,14,30.∴区间(1,62)内所有“企盼数”之和为 2+6+14+30=52.“同正异负” 你注意到了吗结合对数函数的图象,我们可以归纳出下面的重要性质.性质:在对数函数 y=logax(a>0 且 a≠1)中,(1)若 ...