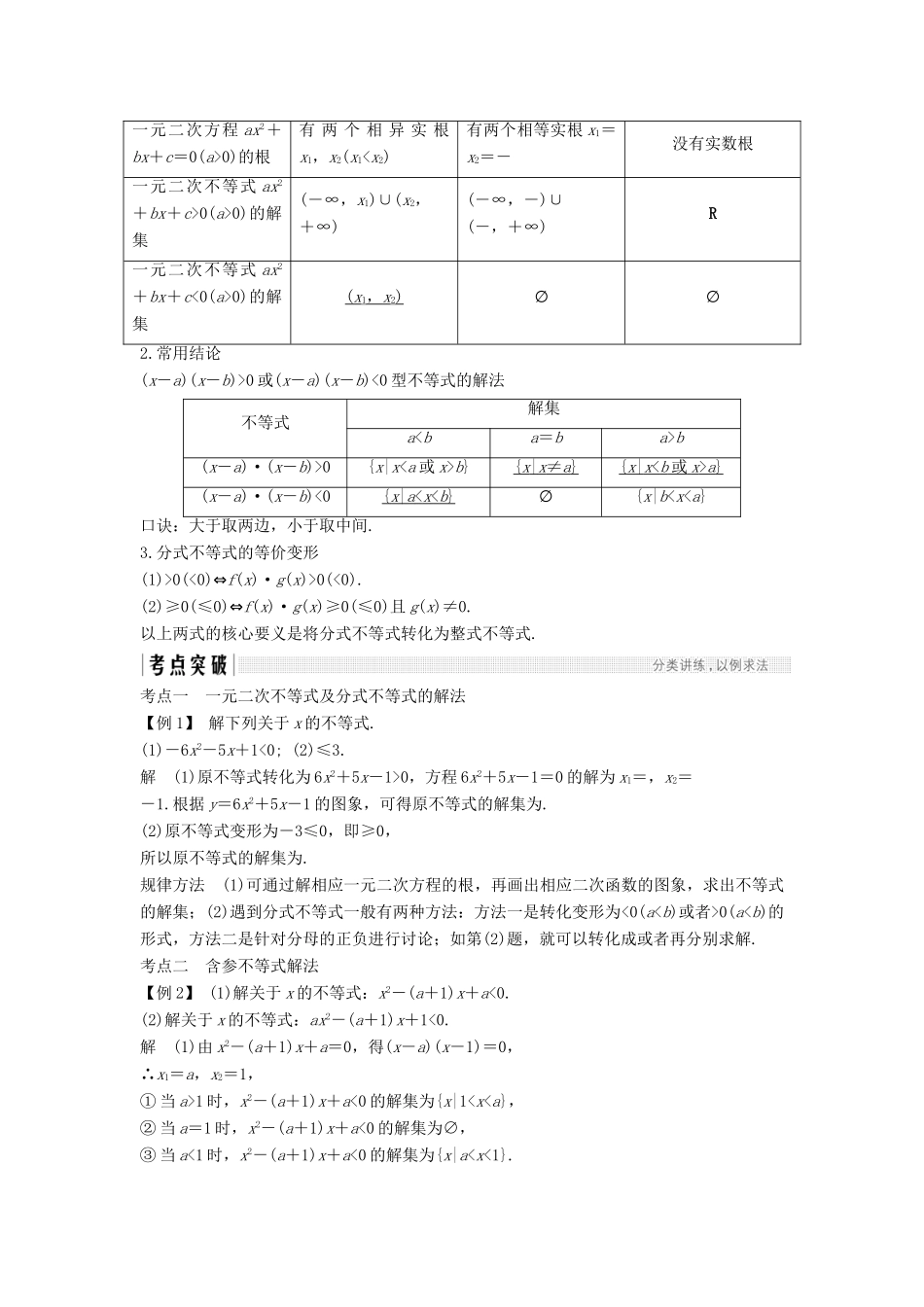
第 40 讲 一元二次不等式考试要求 1.从实际情境中抽象出一元二次不等式模型,一元二次不等式与相应的二次函数、一元二次方程的联系(B 级要求);2.求解一元二次不等式(C 级要求).诊 断 自 测1.(教材改编)不等式 x2-3x-10>0 的解集是________.解析 解方程 x2-3x-10=0 得 x1=-2,x2=5,由于 y=x2-3x-10 的图象开口向上,所以 x2-3x-10>0 的解集为(-∞,-2)∪(5,+∞).答案 (-∞,-2)∪(5,+∞)2.(扬州市 2018 届高三上学期期中)不等式<2 的解集为________.解析 <2,即<0 等价于(1-x)x<0,∴不等式的解集是(-∞,0)∪(1,+∞).答案 (-∞,0)∪(1,+∞)3.(教材改编)若关于 x 的不等式 ax2+bx+2>0 的解集是,则 a+b=________.解析 x1=-,x2=是方程 ax2+bx+2=0 的两个根,∴解得∴a+b=-14.答案 -144.(必修 5P78 例 3 改编)某厂生产一批产品,日销售量 x(单位:件)与货价 p(单位:元/件)之间的关系为 p=160-2x,生产 x 件所需成本 C=500+30x 元.若使得日获利不少于 1300元,则该厂日产量所要满足的条件是__________.解析 由题意得(160-2x)·x-(500+30x)≥1300,解得 20≤x≤45.答案 [20,45]5.(必修 5P80 习题 8 改编)若不等式 x2-2x+k2-2>0 对于任意的 x∈[2,+∞)恒成立,则实数 k 的取值范围是________.解析 由 x2-2x+k2-2>0,得 k2>-x2+2x+2,设 f(x)=-x2+2x+2,f(x)=-(x-1)2+3,当 x≥2,可求得 f(x)max=2,则 k2>f(x)max=2,所以 k>或 k<-答案 (-∞,-)∪(,+∞)知 识 梳 理1.“三个二次”的关系判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数 y=ax2+bx+c(a>0)的图象一元二次方程 ax2+bx+c=0(a>0)的根有 两 个 相 异 实 根x1,x2(x1
0(a>0)的解集(-∞,x1)∪(x2,+∞)(-∞,-)∪(-,+∞)R一元二次不等式 ax2+bx+c<0(a>0)的解集( x 1, x 2)∅∅2.常用结论(x-a)(x-b)>0 或(x-a)(x-b)<0 型不等式的解法不等式解集ab(x-a)·(x-b)>0{x|xb}{ x | x ≠ a } { x | x < b 或 x > a } (x-a)·(x-b)<0{ x | a < x < b } ∅{x|b0(<0)⇔f(x)·g(x)>0(<0).(2)≥0(≤0)⇔f(x)·g(x)≥0(≤0)且 ...