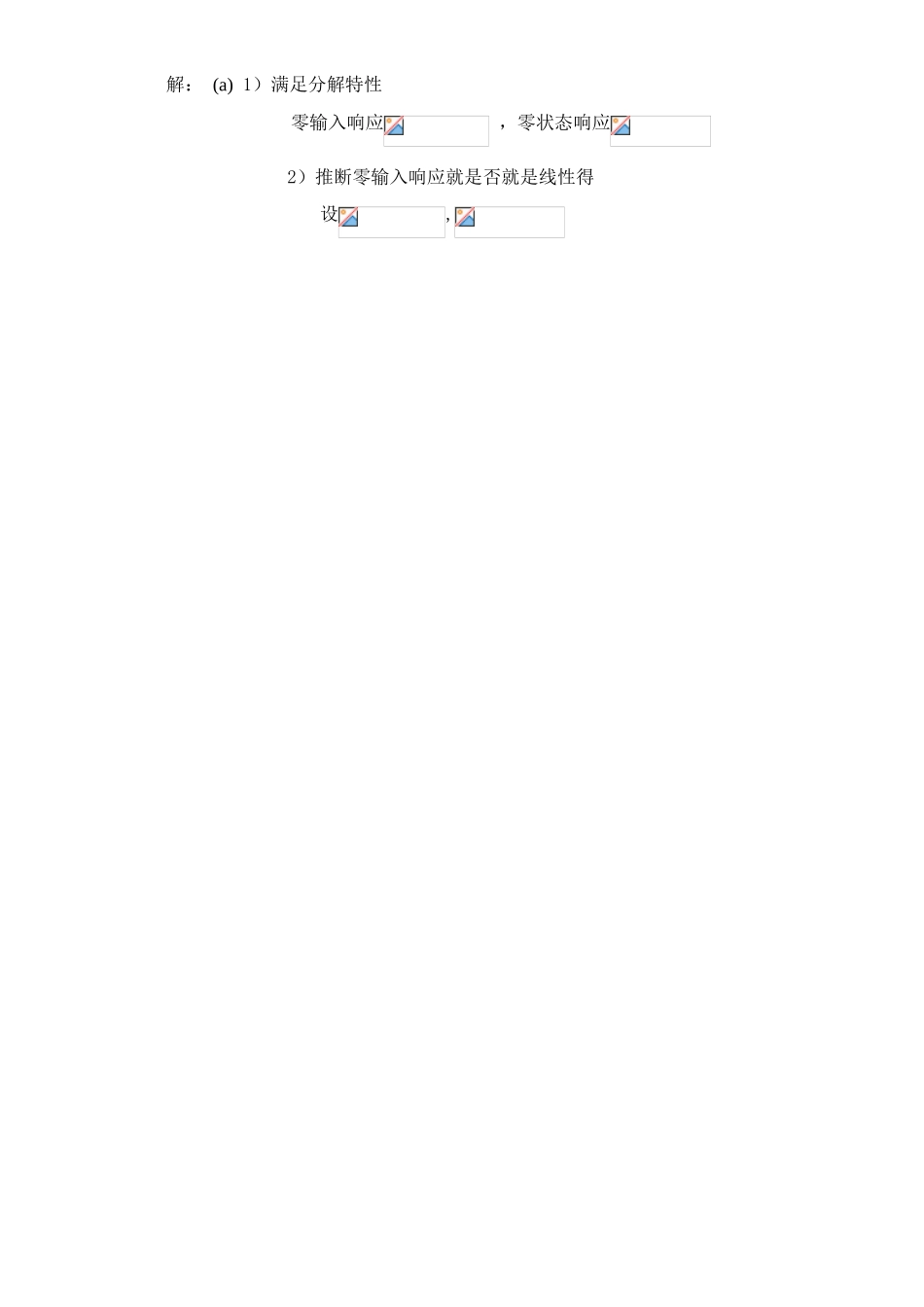
西南交通大学 2025-2025 学年第(2)学期中期考试试卷答案课程代码 课程名称 信号与系统(含实验) 考试时间 120 分钟 一、计算(本题 20 分) (1)已知信号,周期为 2 ,就是能量信号还就是功率信号?功率信号。计算能量或功率为功率 62 、 5W 。 (2)。(3) 已知,为求,选择 b 才能得到正确结果。(a)左移 (b) 右移 (c) 右移(d)左移 解:(a),不能 (b) ,能 (c) ,不能(d),不能 (4) 若系统为无失真传输,则系统函数=。推断系统就是否就是无失真传输系统,假如不就是请指明就是幅度失真还就是相位失真 不就是无失真系统,相 位失真 。 (5) 推断下列系统就是否就是线性系统,给出理由。 (a) (b) (c) 解: (a) 1)满足分解特性零输入响应 ,零状态响应 2)推断零输入响应就是否就是线性得 设,当输入为时输出为所以零输入响应就是非线性得所以该系统为非线性系统(b) 线性系统(c) 线性系统(6) 推断系统就是否就是时不变系统,给出理由。(a) (b) 解:(a)令输入延迟,即,输出为该系统为时变系统(b) 为时变系统二、(本题 12 分)已知系统得微分方程,初始条件为,求:(1)系统函数;(2)单位冲激响应;(3)零输入响应。解:(1) 算子方程: 传输算子 (2) (3) 极点: ,带入初始条件得:,解得: ,三、(10 分)已知线性系统当输入时,系统得零状态响应,求:(1)单位冲激响应;(2)当输入时,系统得零状态响应。解:(1)(2)当输入时,。四、(10 分)作图题。(1) 已知,请画出得波形(注明幅度、时间关键值)。(2) 已知得傅立叶变换就是,请画出信号得振幅频谱与相位频谱图。五、(10 分)(1) 如图所示,求其傅里叶变换。 图1 第五题图 解:(a)或者答案为:tf(t)120-2图 (b)图 (a)(b) 由卷积定理得: (2) 求下列信号得奈奎斯特抽样频率与抽样间隔。 (a) (b) (c) 设 f(t)得最高频率Hz,求信号得奈奎斯特抽样频率与抽样间隔 解:(a) , , ,(b) , , , (c)f(t)得最大频率为 200,f(2t)最大频率为 400,最大频率为 200, 所以:得奈奎斯特抽样频率,抽样间隔。六、求卷积(12 分) 知信号与得波形如下图所示,用图解法计算卷积。解:解: 采纳图解法:(1)变量替换: (4)计 算 1)当时 ,无 重合 区域2) 当时,重合区域为3) 当,重合区域为4) 当且时,重合区域为5) 当时,重合区域为6) 当时,重合区域为 0所以:七 、 ( 10 分 ) 已 知 某 理 想...