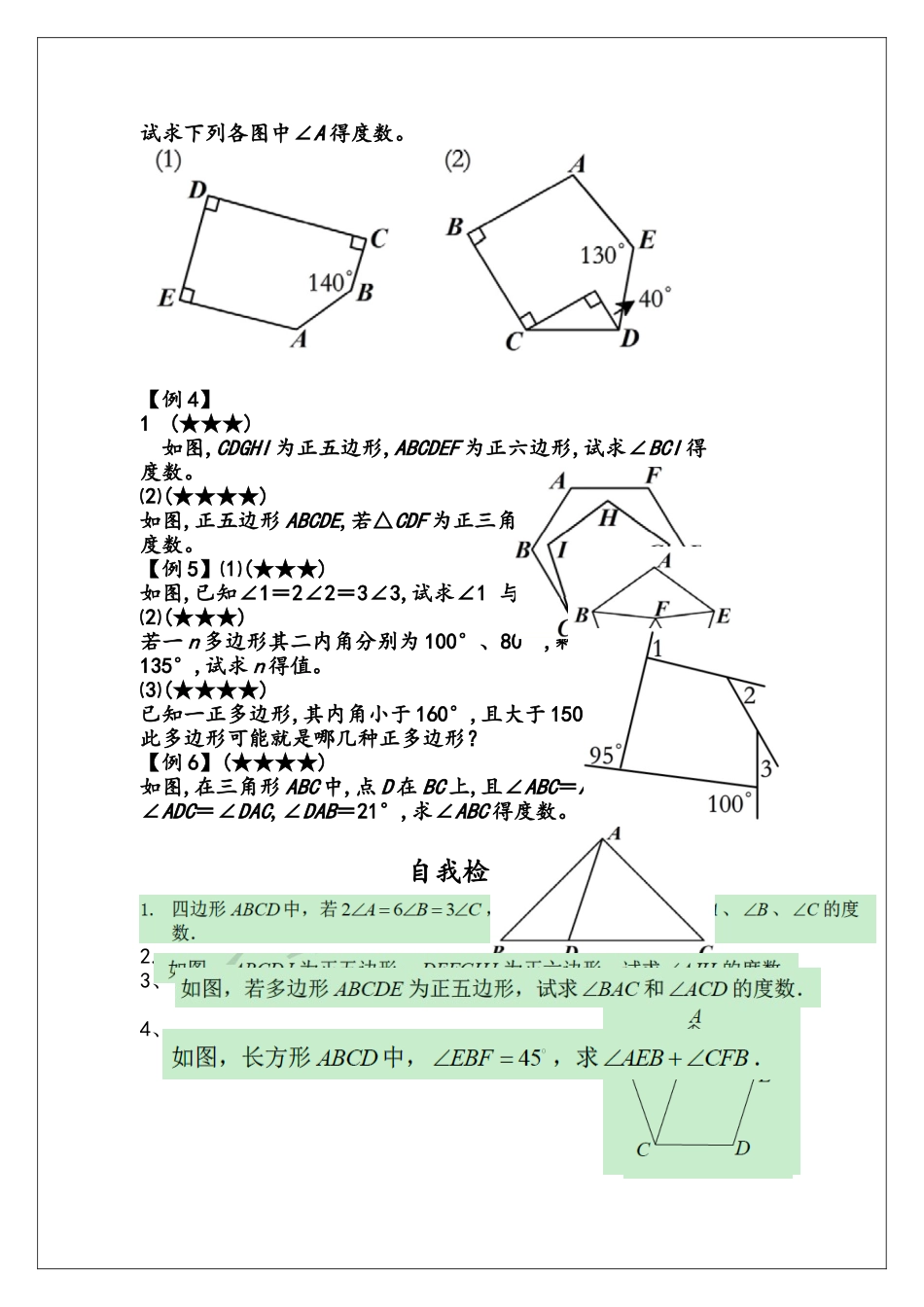
第十三讲 角度得综合应用【教学重难点】根据图形中角度得特征解决相应得问题。【课前预习】根据辅导书相应地给孩子预习得内容。一. 角得分类(1)我们熟悉得:周角,平角,直角,锐角与钝角。(2)我们不熟悉得余角:两角与等于直角时,其中一个角叫做另一个角得余角。这两个角叫做互为余角。补角:两角与等于平角时,其中一个角就是另一个角得补角。这两个角叫做互为补角。对顶角:把一个角得两边分别向相反方向延长,这两条延长线所夹得角,叫做原角得对顶角。【例 1】⑴(★★)如图,在直角∠AOB 内有两条射线 OC,OD。已知∠1 比∠2 小 10°,∠3 比∠2 大 10°,则∠3=_______ 。⑵(★★★)(“希望杯”全国数学邀请赛四年级第 1 试)直线 AB、CD 相交,若∠1、∠2 与∠3 得关系图所示。则∠3-∠1= ______ 。n 边形得内角与=(n2)×1800 多边形得外角与=3600【例 2】(★★★)(“希望杯”全国数学邀请赛四年级第 1 试)如图,∠1=∠2,∠3=∠4,∠5=130°那么∠A=_______ 度。【例 3】(★★★)试求下列各图中∠A 得度数。【例 4】1 (★★★)如图,CDGHI 为正五边形,ABCDEF 为正六边形,试求∠BCI 得度数。⑵(★★★★)如图,正五边形 ABCDE,若△CDF 为正三角形,试求∠BFE 得度数。【例 5】⑴(★★★)如图,已知∠1=2∠2=3∠3,试求∠1 与∠3 。⑵(★★★)若一 n 多边形其二内角分别为 100°、80°,剩下得内角均为135°,试求 n 得值。⑶(★★★★)已知一正多边形,其内角小于 160°,且大于 150°,试求出此多边形可能就是哪几种正多边形?【例 6】(★★★★)如图,在三角形 ABC 中,点 D 在 BC 上,且∠ABC=ACB,∠ADC=∠DAC,∠DAB=21°,求∠ABC 得度数。自我检测2.、3、4、