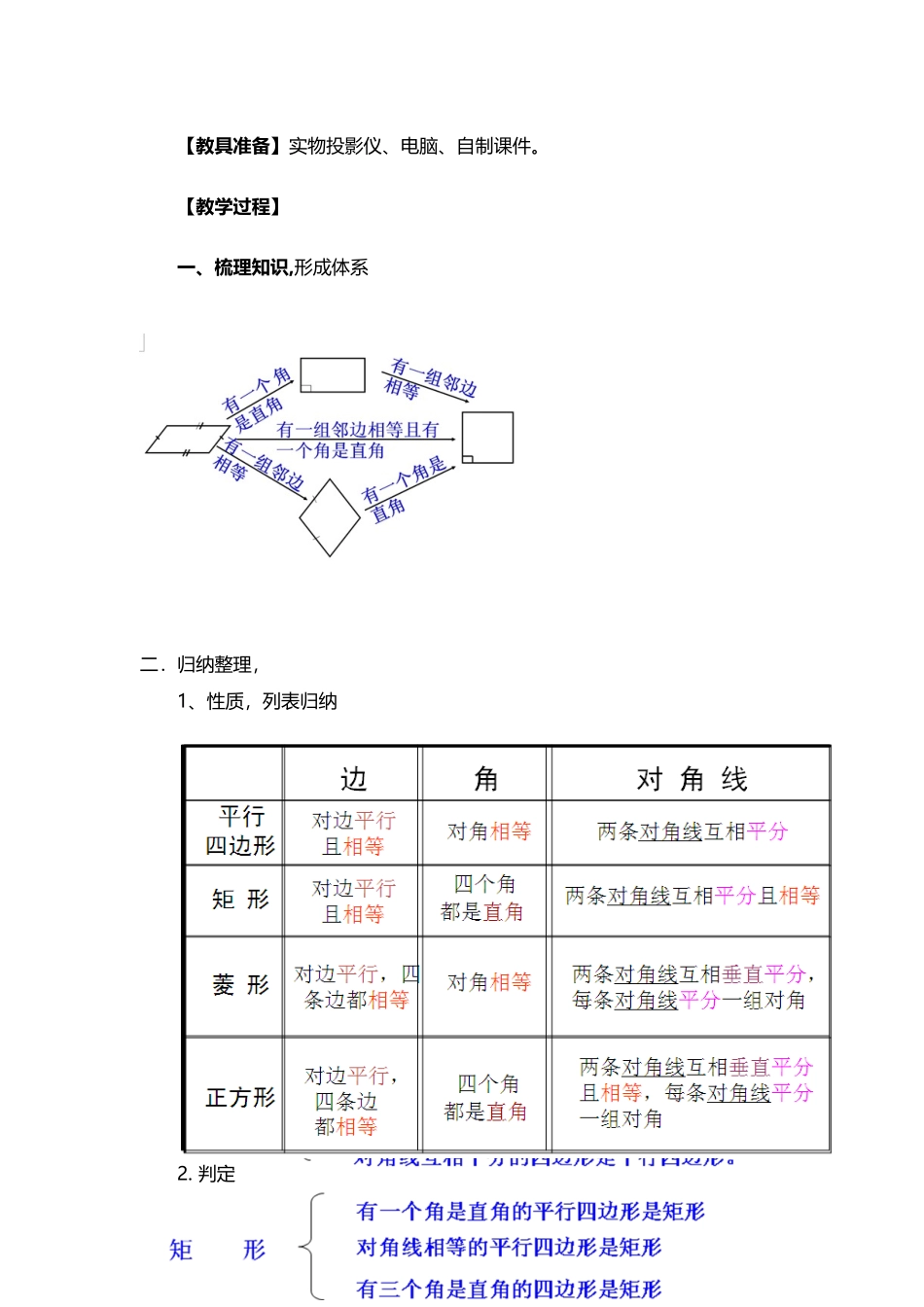
《平行四边形》复习课教案(6 页)Good is good, but better carries it.精益求精,善益求善。《平行四边形》复习课教案乌鲁木齐市第十六中学 万敏霞【教学目标】1、通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习平行四边形与各种特别平行四边形的定义、性质、判定方法;2、正确理解平行四边形与各种特别平行四边形的联系与区别,在反思和沟通过程中,逐渐建立知识体系;3、引导学生独立思考,通过归纳、概括、实践等系统数学活动,感受获得成功的体验,形成科学的学习习惯。【教学重点】1、平行四边形与各种特别平行四边形的区别。2、梳理平行四边形、矩形、菱形、正方形的知识体系及应用方法。【教学难点】平行四边形与各种特别平行四边形的定义、性质、判定的综合运用。【教学模式】梳理知识-----查漏补缺 -----综合训练-----基础巩固-----典型例题【教具准备】实物投影仪、电脑、自制课件。【教学过程】一、梳理知识,形成体系二.归纳整理,1、性质,列表归纳2. 判定三、查漏补缺,讲练结合(一)基础巩固(二)一题多解,培育应变能力典例 1.在□ ABCD 中,BM⊥AC, DN⊥AC,垂足分别为点 M,N.求证:四边形 BMDN 是平行四边形 (三)综合练习,提高解题能力典例 2.已知:如图,在△ABC 中,AB=AC,AD⊥BC,垂足为点 D,AN是△ABC 外角∠CAM 的平分线,CE⊥AN,垂足为点 E,(1)求证:四边形 ADCE 为矩形;(2)当△ABC 满足什么条件时,四边形 ADCE 是一个正方形?并给出证明.典例 3 .已知如图,菱形 ABCD 的对角线 AC、BD 交于点O,AC=6,BD=8,求菱形的高。典例 4 过正方形 ABCD 对角线 BD 上一点 P,作 PE⊥BC 于 E,PF⊥CD于 F求证:AP=EF(四)思维拓展,总结规律顺次连接平行四边形各边中点所得的四边形是____________顺次连接矩形各边中点所得的四边形是_____顺次连接菱形各边中点所得的四边形是______请你说说把具有什么特点的四边形的各边中点连接起来能得到正方形呢?四.课堂小结五.作业:课本 P67 2,5 P67 7 8…;(.~*>&—【/)}~;`&*—"—:(]$\、>】`