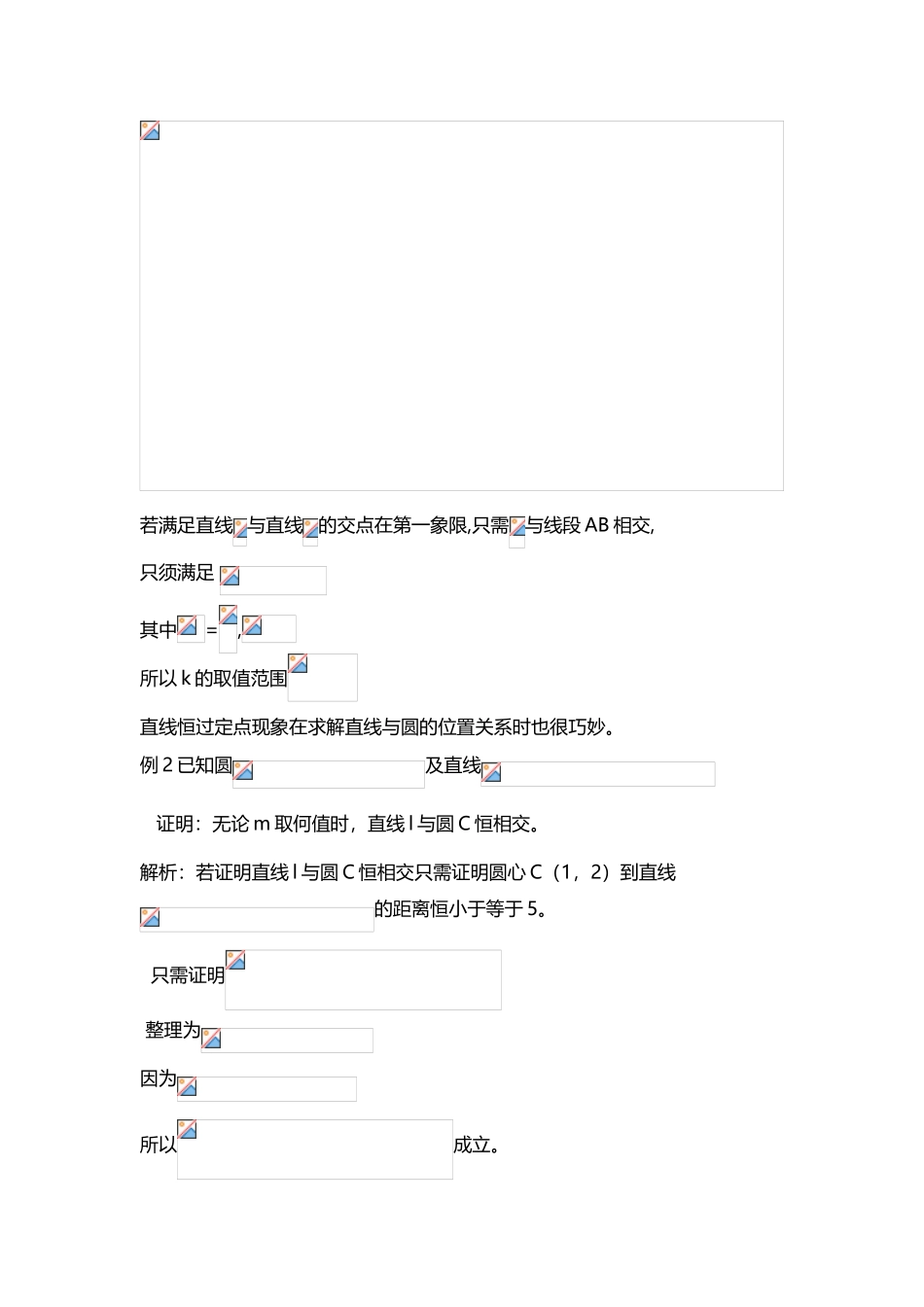
带参数的直线方程恒过定点现象在解题中的应用(2 页)Good is good, but better carries it.精益求精,善益求善。带参数的直线方程恒过定点现象在解题中的应用张家口市第一中学 (075000) 田盟盟 (tel:15832350180)关于直线方程的各种形式学生们都以非常熟悉,但是,当遇到带参数的直线方程时,由于没意识到此类直线方程的特征,所以解起题来方法很笨拙。例 1 k 为何值时,直线与直线的交点在第一象限? 分析:两直线的交点可通过解方程组得到(用字母 k 表示),然后利用x>0,y>0 进行求解.具体解法如下: 由 得 因为两直线的交点在第一象限所以 解得即当时,两直线的交点在第一象限.此种解法学生容易想到,但是计算量比较大,而且涉及分式不等式的解法,所以容易出错.但假如意识到此直线恒过定点(-3,-2),利用数形结合的思想解决此题将非常方便.如图:若满足直线 与直线的交点在第一象限,只需与线段 AB 相交,只须满足 其中=,所以 k 的取值范围直线恒过定点现象在求解直线与圆的位置关系时也很巧妙。例 2 已知圆及直线 证明:无论 m 取何值时,直线 l 与圆 C 恒相交。解析:若证明直线 l 与圆 C 恒相交只需证明圆心 C(1,2)到直线的距离恒小于等于 5。 只需证明 整理为因为所以成立。若意识到直线恒过定点,可得到新的解法。如下:解法(二)直线整理为 所以直线恒过直线 x+y-4=0 与直线 2x+y-7=0 交点 M(3,1)而所以点 M(3,1)在圆内所以无论 m 取何值直线都与圆相交。带参数的直线方程在解题中常常出现,若能适时的应用直线恒过定点这一现象,可以简化解题过程,优化解题思路,起到事半功倍的效果。,;…。`^}~*'¥:&??[{;¥.…:】]/.。!#【