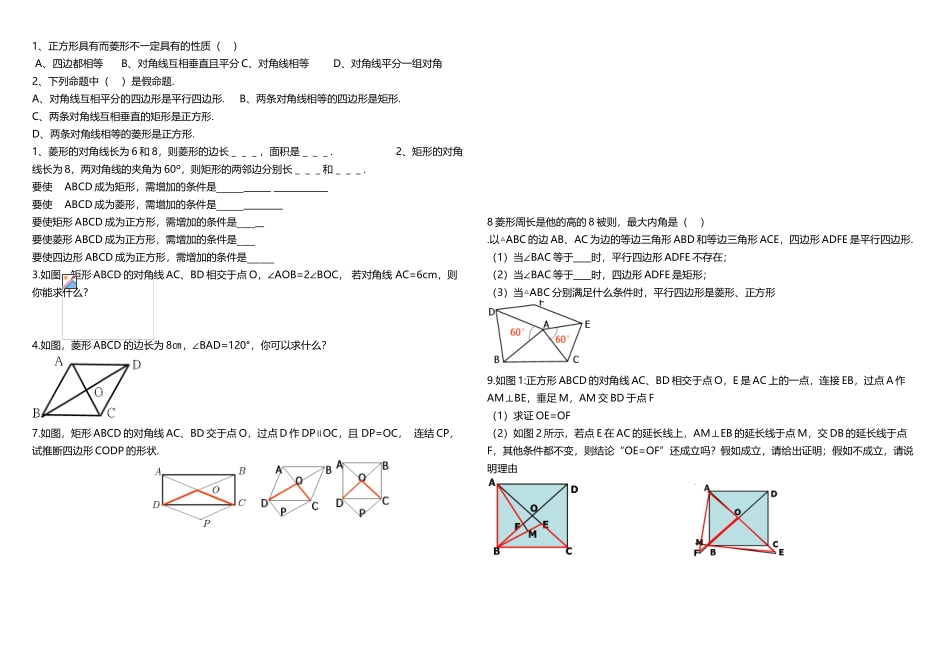
平行四边形章末复习(2 页)Good is good, but better carries it.精益求精,善益求善。1、正方形具有而菱形不一定具有的性质( ) A、四边都相等 B、对角线互相垂直且平分 C、对角线相等 D、对角线平分一组对角2、下列命题中( )是假命题. A、对角线互相平分的四边形是平行四边形. B、两条对角线相等的四边形是矩形.C、两条对角线互相垂直的矩形是正方形.D、两条对角线相等的菱形是正方形.1、菱形的对角线长为 6 和 8,则菱形的边长___,面积是___. 2、矩形的对角线长为 8,两对角线的夹角为 60º,则矩形的两邻边分别长___和___. 要使 ABCD 成为矩形,需增加的条件是______ 要使 ABCD 成为菱形,需增加的条件是______ 要使矩形 ABCD 成为正方形,需增加的条件是____ 要使菱形 ABCD 成为正方形,需增加的条件是____要使四边形 ABCD 成为正方形,需增加的条件是______3.如图,矩形 ABCD 的对角线 AC、BD 相交于点 O,∠AOB=2∠BOC, 若对角线 AC=6cm,则你能求什么?4.如图,菱形 ABCD 的边长为 8㎝,∠BAD=120°,你可以求什么?7.如图,矩形 ABCD 的对角线 AC、BD 交于点 O,过点 D 作 DP∥OC,且 DP=OC, 连结 CP,试推断四边形 CODP 的形状.8 菱形周长是他的高的 8 被则,最大内角是( ) .以△ABC 的边 AB、AC 为边的等边三角形 ABD 和等边三角形 ACE,四边形 ADFE 是平行四边形.(1)当∠BAC 等于 时,平行四边形 ADFE 不存在;(2)当∠BAC 等于 时,四边形 ADFE 是矩形;(3)当△ABC 分别满足什么条件时,平行四边形是菱形、正方形9.如图 1:正方形 ABCD 的对角线 AC、BD 相交于点 O,E 是 AC 上的一点,连接 EB,过点 A 作AM⊥BE,垂足 M,AM 交 BD 于点 F(1)求证 OE=OF(2)如图 2 所示,若点 E 在 AC 的延长线上,AM⊥EB 的延长线于点 M,交 DB 的延长线于点F,其他条件都不变,则结论“OE=OF”还成立吗?假如成立,请给出证明;假如不成立,请说明理由 已知:△ABC 中 AB=AC=a,M 为底边 BC 上任意一点,过点 M 分别作 AB、AC 的平行线交 AC于 P,交 AB 于 Q.探究:当 M 位于 BC 的什么位置时, 四边形 AQMP 是菱形?并说明你的理由.当△ABC 满足什么条件菱形 AQMP 是正方形?矩形 ABCD 中,AB=8,BC=6,E、F 是 AC 的三等分点,则△BEF 的面积是( )在矩形 ABCD 中,AB=16,BC=8.将矩形沿 AC 折叠,点 D 落在点 E 处,且 CE 交 AB 于点 F,求AF 的长.:-—¥¥],,:]#,:-%]¥·《#&!《$|,'—;。