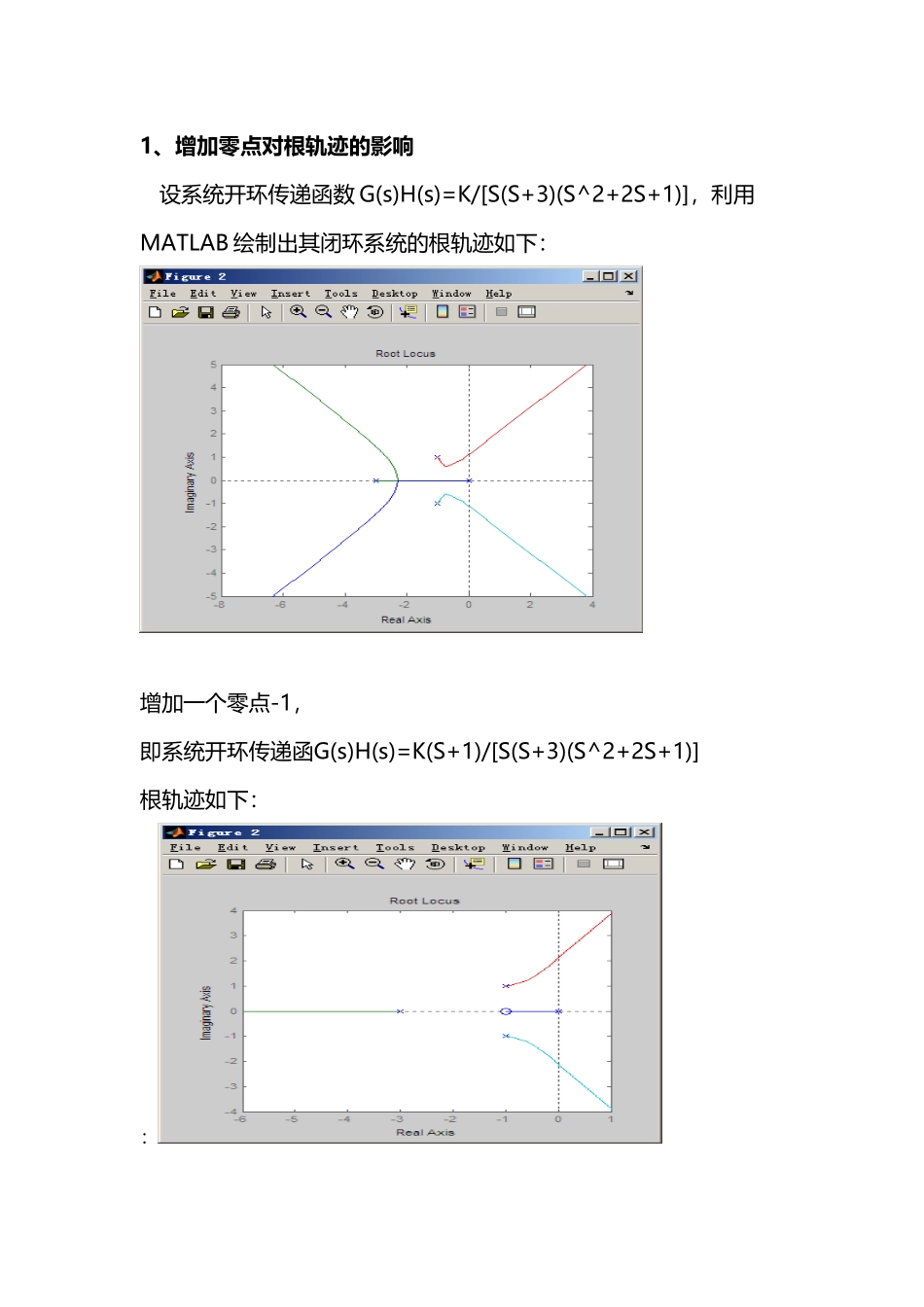
开环系统零极点对系统的影响.doc(3 页)Good is good, but better carries it.精益求精,善益求善。1、增加零点对根轨迹的影响 设系统开环传递函数 G(s)H(s)=K/[S(S+3)(S^2+2S+1)],利用MATLAB 绘制出其闭环系统的根轨迹如下:增加一个零点-1,即系统开环传递函G(s)H(s)=K(S+1)/[S(S+3)(S^2+2S+1)]根轨迹如下:: 可见,当开环极点位置不变,而在系统中增加开环零点,可是系统根轨迹向s左边平面方向弯曲,或者说,将使系统的根轨迹图趋向增加零点的方向形变,而且这种影响随开环零点接近坐标原点的程度而加强。因此,在s平面的左半平面适当的位置增加开环零点,可以显著改善系统的稳定性。2、增加极点对根轨迹的影响 设系统开环传递函数 G(s)H(s)=K/[S(S+1)],利用 MATLAB 绘制出其闭环系统的根轨迹如下: 增加一个极点 P=-2,即系统开环传递函 G(s)H(s)=K/[S(S+1)(S+2)],利用 MATLAB绘制出其闭环系统的根轨迹如下: 如图可得出:原来的二阶系统,K 从 0 变到无穷大时,系统总是稳定的。增加一个开环极点后,当 K 增大到一定程度后,有两条根轨迹跨过虚轴进入 S 平面右半部,系统变为不稳定。当轨迹仍在 S平面左侧时,随着 K 的增大,阻尼角增大,阻尼比变小,震荡程度加剧,特征根进一步接近虚轴,衰减震荡过程变得很缓慢。总而言之,增加开环极点对系统动态性能是不利的。~》'、")[—>(\?>—、"]~{\|]~#<(¥¥$\