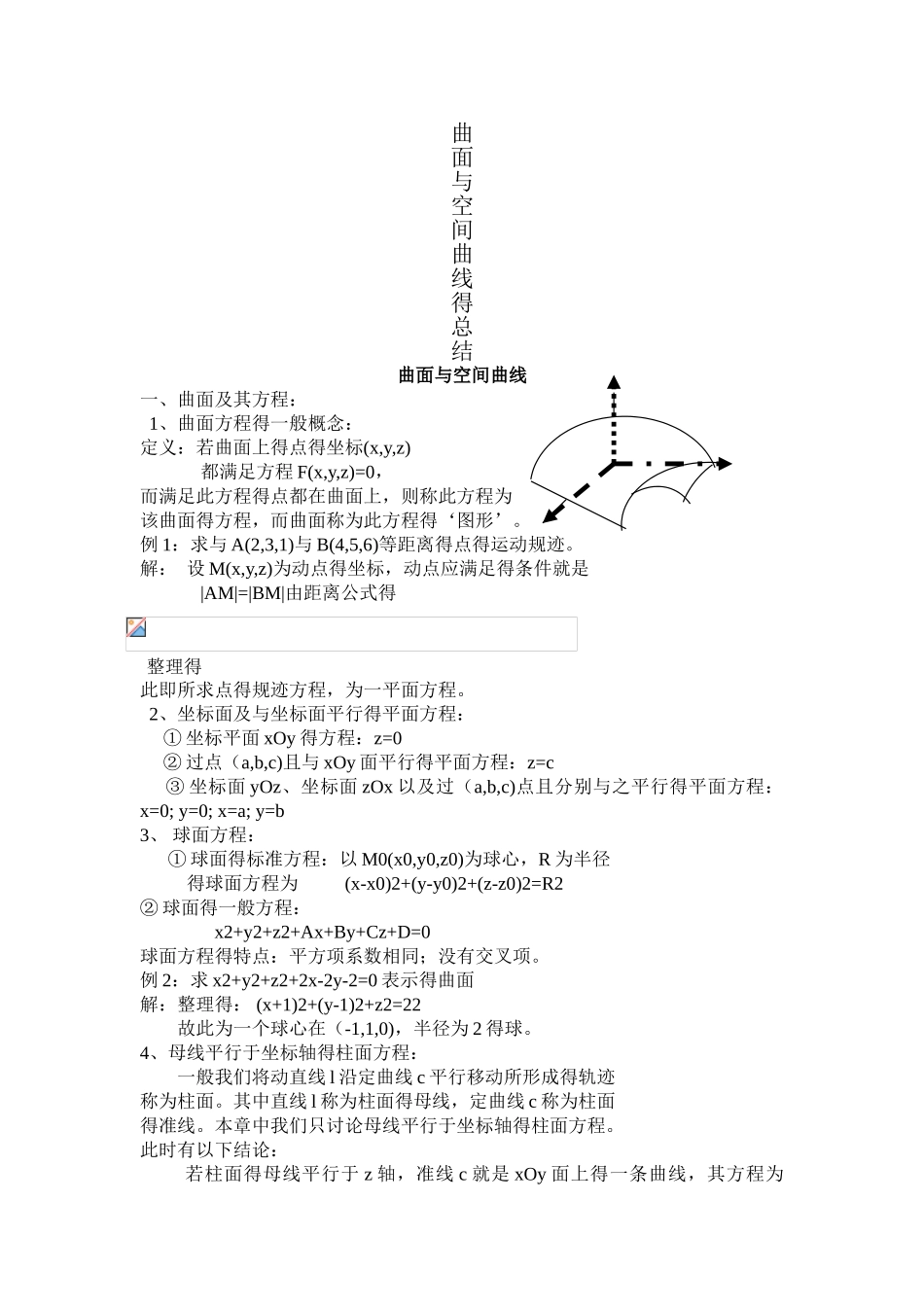
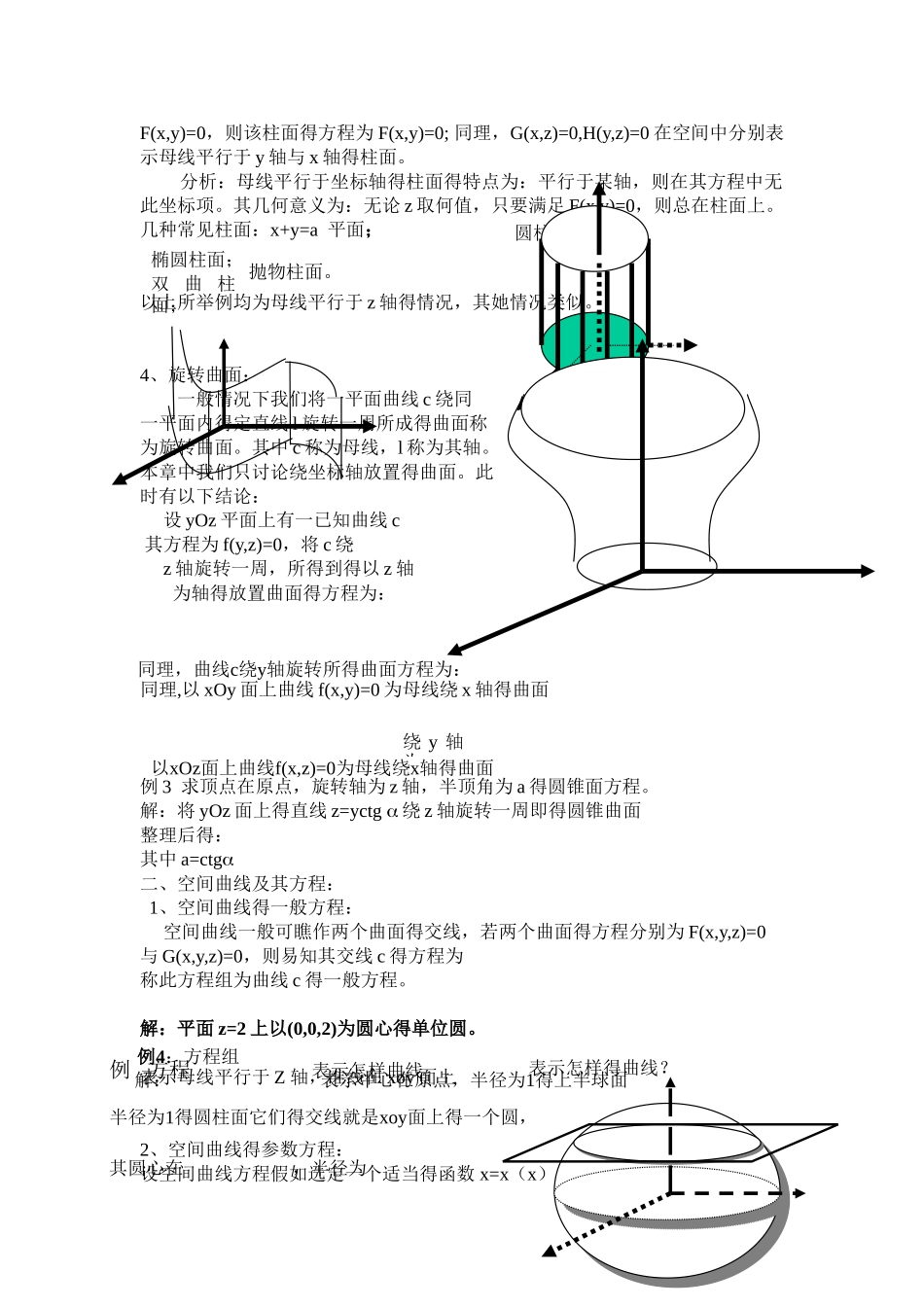
曲面与空间曲线得总结曲面与空间曲线一、曲面及其方程: 1、曲面方程得一般概念: 定义:若曲面上得点得坐标(x,y,z) 都满足方程 F(x,y,z)=0,而满足此方程得点都在曲面上,则称此方程为该曲面得方程,而曲面称为此方程得‘图形’。例 1:求与 A(2,3,1)与 B(4,5,6)等距离得点得运动规迹。解: 设 M(x,y,z)为动点得坐标,动点应满足得条件就是 |AM|=|BM|由距离公式得此即所求点得规迹方程,为一平面方程。 2、坐标面及与坐标面平行得平面方程: ① 坐标平面 xOy 得方程:z=0 ② 过点(a,b,c)且与 xOy 面平行得平面方程:z=c ③ 坐标面 yOz、坐标面 zOx 以及过(a,b,c)点且分别与之平行得平面方程:x=0; y=0; x=a; y=b 3、 球面方程: ① 球面得标准方程:以 M0(x0,y0,z0)为球心,R 为半径 得球面方程为 (x-x0)2+(y-y0)2+(z-z0)2=R2② 球面得一般方程: x2+y2+z2+Ax+By+Cz+D=0球面方程得特点:平方项系数相同;没有交叉项。例 2:求 x2+y2+z2+2x-2y-2=0 表示得曲面解:整理得: (x+1)2+(y-1)2+z2=22 故此为一个球心在(-1,1,0),半径为 2 得球。4、母线平行于坐标轴得柱面方程: 一般我们将动直线 l 沿定曲线 c 平行移动所形成得轨迹称为柱面。其中直线 l 称为柱面得母线,定曲线 c 称为柱面得准线。本章中我们只讨论母线平行于坐标轴得柱面方程。此时有以下结论: 若柱面得母线平行于 z 轴,准线 c 就是 xOy 面上得一条曲线,其方程为整理得椭圆柱面;双 曲 柱面;抛物柱面。F(x,y)=0,则该柱面得方程为 F(x,y)=0; 同理,G(x,z)=0,H(y,z)=0 在空间中分别表示母线平行于 y 轴与 x 轴得柱面。 分析:母线平行于坐标轴得柱面得特点为:平行于某轴,则在其方程中无此坐标项。其几何意义为:无论 z 取何值,只要满足 F(x,y)=0,则总在柱面上。几种常见柱面:x+y=a 平面;以上所举例均为母线平行于 z 轴得情况,其她情况类似。 4、旋转曲面: 一般情况下我们将一平面曲线 c 绕同一平面内得定直线 l 旋转一周所成得曲面称为旋转曲面。其中 c 称为母线,l 称为其轴。本章中我们只讨论绕坐标轴放置得曲面。此时有以下结论: 设 yOz 平面上有一已知曲线 c 其方程为 f(y,z)=0,将 c 绕 z 轴旋转一周,所得到得以 z 轴 为轴得放置曲面得方程为: 同理,以 xOy 面上曲线 f(x,y)=0 为母线绕 x 轴得曲面 例 3 求顶点在原点,旋转轴为 z 轴,半顶角为...