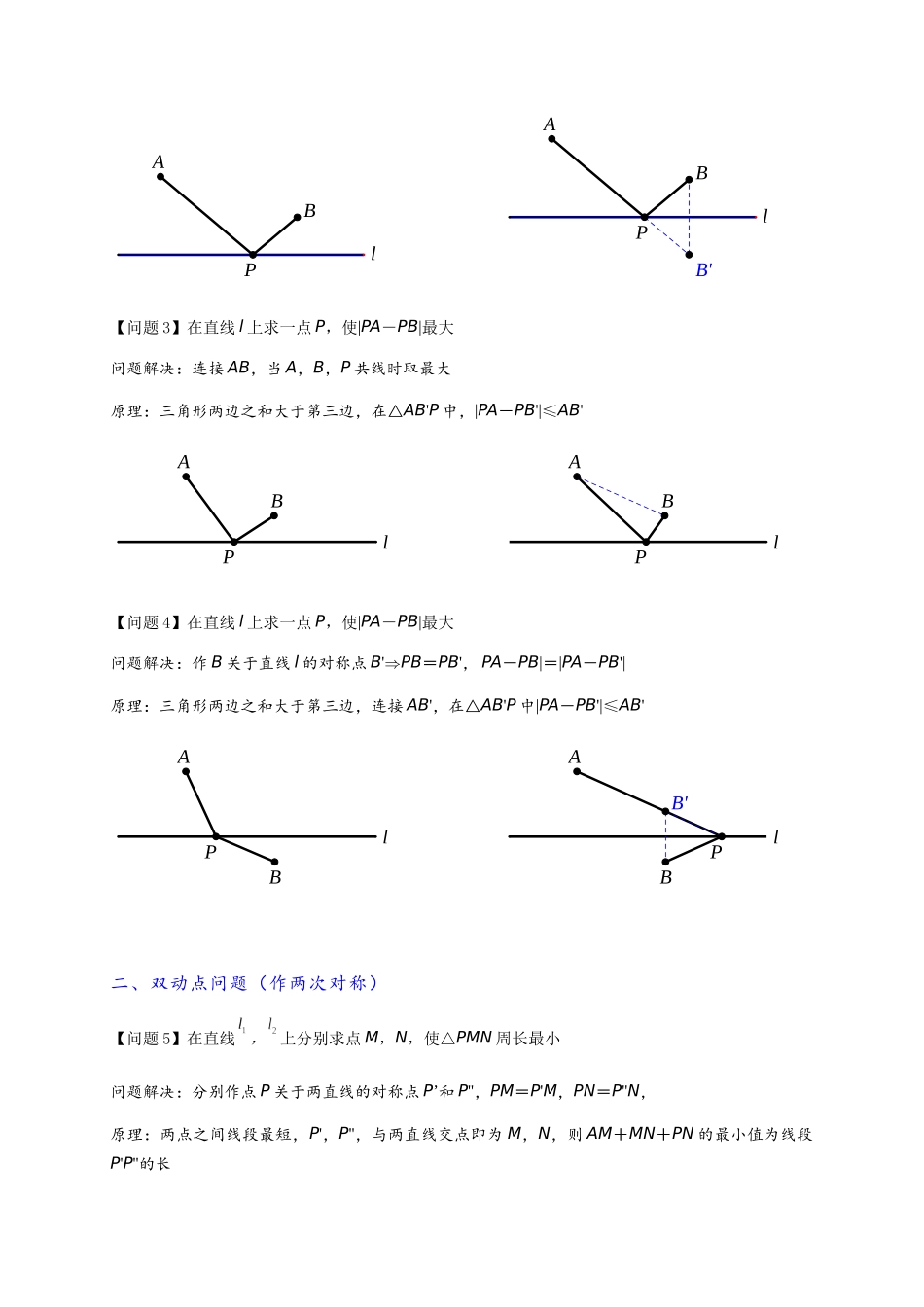
专题 2-1 将军饮马等 8 类常见最值问题 01题型·解读题型一 两定一动型(线段和差最值问题)题型二 双动点最值问题(两次对称)题型三 动线段问题:造桥选址(构造平行四边形)题型四 垂线段最短题型五 相对运动平移型将军饮马题型六 通过瓜豆得出轨迹后将军饮马题型七 化斜为直,斜大于直题型八 构造二次函数模型求最值满分·技巧02一、单动点问题【问题 1】在直线 l 上求一点 P,使 PA+PB 最小问题解决:连接 AB,与 l 交点即为 P,两点之间线段最短 PA+PB 最小值为 ABlABlPAB【问题 2】在直线 l 上求一点 P,使 PA+PB 最小问题解决:作 B 关于 l 的对称点 B'⇒PB=PB',则 PA+PB=PA+PB',当 A,P,B'共线时取最小,原理:两点之间线段最短,即 PA+PB 最小值为 AB'lBAPlB'BAP【问题 3】在直线 l 上求一点 P,使|PA-PB|最大问题解决:连接 AB,当 A,B,P 共线时取最大原理:三角形两边之和大于第三边,在△AB'P 中,|PA-PB'|≤AB'lBAPlBAP【问题 4】在直线 l 上求一点 P,使|PA-PB|最大问题解决:作 B 关于直线 l 的对称点 B'⇒PB=PB',|PA-PB|=|PA-PB'|原理:三角形两边之和大于第三边,连接 AB',在△AB'P 中|PA-PB'|≤AB'lBAPlB'BAP二、双动点问题(作两次对称)【问题 5】在直线,上分别求点 M,N,使△PMN 周长最小问题解决:分别作点 P 关于两直线的对称点 P’和 P'',PM=P'M,PN=P''N,原理:两点之间线段最短,P',P'',与两直线交点即为 M,N,则 AM+MN+PN 的最小值为线段P'P''的长l1l2PNMl1l2P''P'PNM【问题 6】P,Q 为定点,在直线,上分别求点 M,N,使四边形 PQMN 周长最小问题解决:分别作点 P,Q 关于直线,的对称点 P’和 Q',PM=P'M,QN=Q'N原理:两点之间线段最短,连接 P'Q',与两直线交点即为 M,N,则 PM+MN+QN 的最小值为线段 P'Q'的长,周长最小值为 P'Q'+PQl1l2PQNMl1l2Q'P'PQNM【问题 7】A,B 分别为,上的定点,M,N 分别为,上的动点,求最小值问题解决:分别作,关于,的对称点,,则,,即所求原理:两点之间距离最短,A',N,M,B'共线时取最小,则 AN+MN+BM=A'N+MN+B'M≤A'B'l2l1NMABl2l1A'B'NMAB三、动线段问题(造桥选址)【问题 8】直线 m∥n,在 m,n 上分别求点 M,N,使 MN⊥m,且 AM+MN+BN 的最小值问题解决:将点 B 向上平移 MN 的长度单位得 B',连接 B'M,...