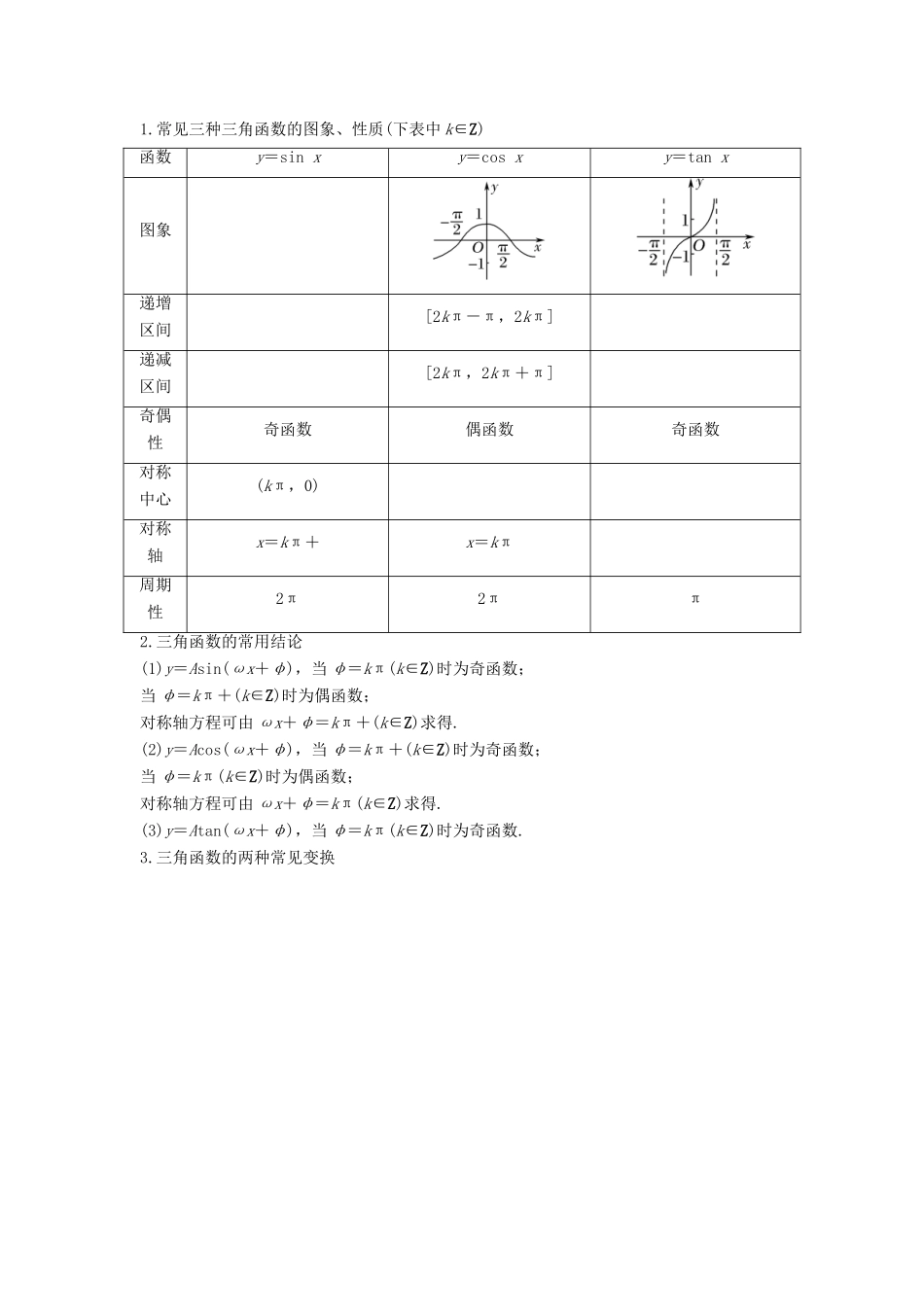
第 1 讲 三角函数的图象与性质高考定位 三角函数的图象与性质是高考考查的重点和热点内容,主要从以下两个方面进行考查:1.三角函数的图象,主要涉及图象变换问题以及由图象确定解析式问题,主要以选择题、填空题的形式考查;2.利用三角函数的性质求解三角函数的值、参数、最值、值域、单调区间等,主要以解答题的形式考查. 真 题 感 悟 1.(2016·浙江卷)设函数 f(x)=sin2x+bsin x+c,则 f(x)的最小正周期( )A.与 b 有关,且与 c 有关 B.与 b 有关,但与 c 无关C.与 b 无关,且与 c 无关 D.与 b 无关,但与 c 有关解析 因为 f(x)=sin2x+bsin x+c=-+bsin x+c+,其中当 b=0 时,f(x)=-+c+,f(x)的周期为 π;b≠0 时,f(x)的周期为 2π,即 f(x)的周期与 b 有关但与 c 无关,故选 B.答案 B2.(2017·全国Ⅲ卷)函数 f(x)=sin+cos 的最大值为( )A. B.1 C. D.解析 cos =cos=sin,则 f(x)=sin+sin=sin,函数的最大值为.答案 A3.(2018·天津卷)将函数 y=sin 的图象向右平移个单位长度,所得图象对应的函数( )A.在区间上单调递增B.在区间上单调递减C.在区间上单调递增D.在区间上单调递减解析 把函数 y=sin 的图象向右平移个单位长度得函数 g(x)=sin=sin 2x 的图象,由-+2kπ≤2x≤+2kπ(k∈Z)得-+kπ≤x≤+kπ(k∈Z),令 k=1,得≤x≤,即函数 g(x)=sin 2x 的一个单调递增区间为,故选 A.答案 A4.(2016·浙江卷)已知 2cos2x+sin 2x=Asin(ωx+φ)+b(A>0),则 A=________,b=________.解析 2cos2x+sin 2x=cos 2x+1+sin 2x=+1=sin+1=Asin(ωx+φ)+b(A>0),∴A=,b=1.答案 1考 点 整 合1.常见三种三角函数的图象、性质(下表中 k∈Z)函数y=sin xy=cos xy=tan x图象递增区间[2kπ-π,2kπ]递减区间[2kπ,2kπ+π]奇偶性奇函数偶函数奇函数对称中心(kπ,0)对称轴x=kπ+x=kπ周期性2π2ππ2.三角函数的常用结论(1)y=Asin(ωx+φ),当 φ=kπ(k∈Z)时为奇函数;当 φ=kπ+(k∈Z)时为偶函数;对称轴方程可由 ωx+φ=kπ+(k∈Z)求得.(2)y=Acos(ωx+φ),当 φ=kπ+(k∈Z)时为奇函数;当 φ=kπ(k∈Z)时为偶函数;对称轴方程可由 ωx+φ=kπ(k∈Z)求得.(3)y=Atan(ωx+φ),当 φ=kπ(k∈Z)时为奇函数.3.三角函数的两种常见变换热点一 三角函数的图象【例 1】 函数 f(x)=...