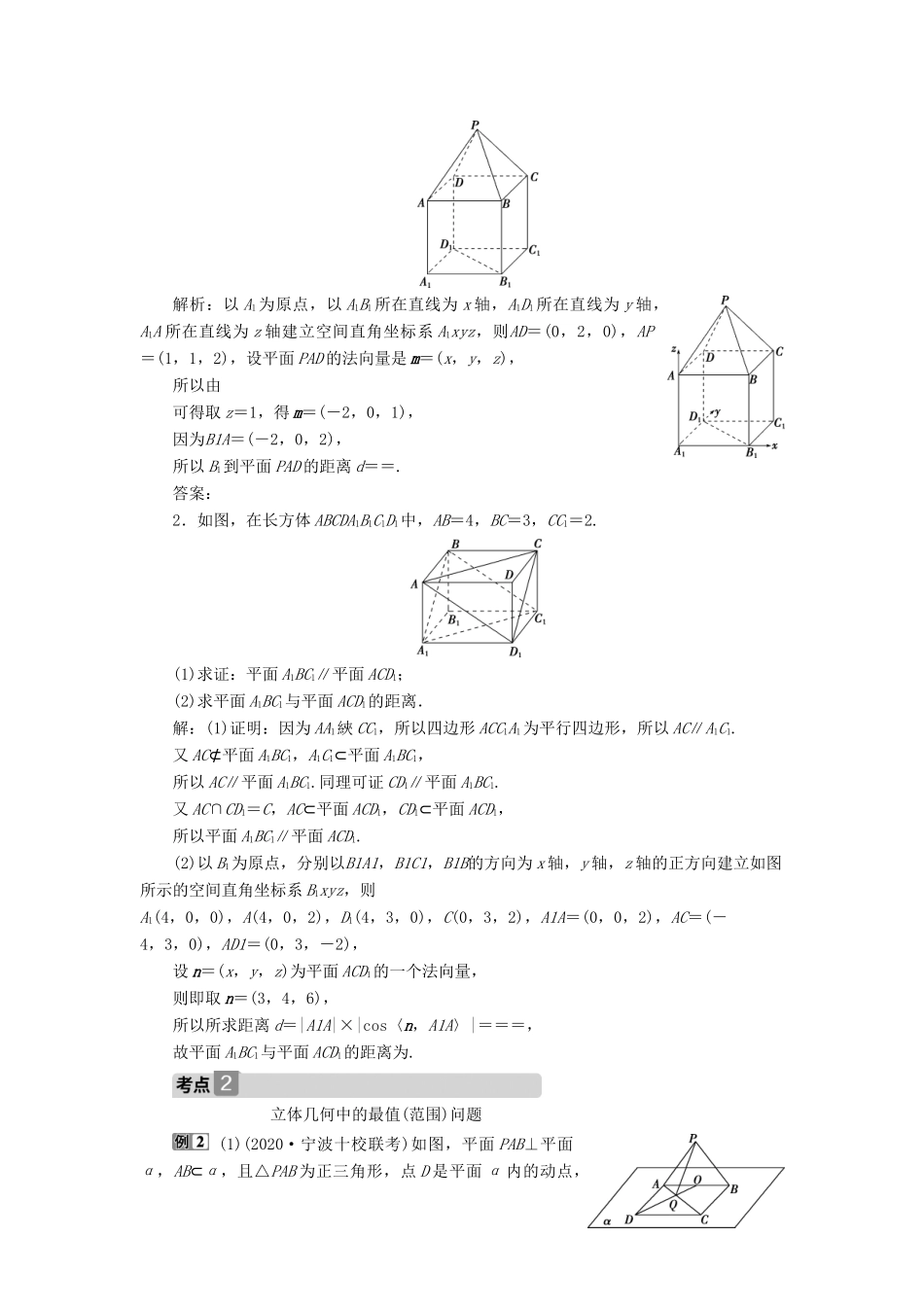
第 2 课时 空间距离与立体几何中的最值(范围)问题(选用) 空间中的距离问题 如图,平面 PAD⊥平面 ABCD,四边形 ABCD 为正方形,△PAD 是直角三角形,且PA=AD=2,点 E,F,G 分别是线段 PA,PD,CD 的中点.(1)求证:平面 EFG⊥平面 PAB;(2)求点 A 到平面 EFG 的距离.【解】 如图,建立空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).(1)证明:因为EF=(0,1,0),AP=(0,0,2),AB=(2,0,0),所以EF·AP=0×0+1×0+0×2=0,EF·AB=0×2+1×0+0×0=0,所以 EF⊥AP,EF⊥AB.又因为 AP,AB⊂平面 PAB,且 PA∩AB=A,所以 EF⊥平面 PAB.又 EF⊂平面 EFG,所以平面 EFG⊥平面 PAB.(2)设平面 EFG 的一个法向量为 n=(x,y,z),则所以取 n=(1,0,1),又AE=(0,0,1),所以点 A 到平面 EFG 的距离 d===.(1)空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离.① 点点距:点与点的距离,以这两点为起点和终点的向量的模;②点线距:点 M 到直线 a 的距离,若直线的方向向量为 a,直线上任一点为 N,则点 M 到直线 a 的距离为 d=|MN|·sin〈MN,a〉;③线线距:两平行线间的距离转化为点线距离,两异面直线间的距离转化为点面距离或者直接求公垂线段的长度;④点面距:点 M 到平面 α 的距离,若平面 α的法向量为 n,平面 α 内任一点为 N,则点 M 到平面 α 的距离 d=|MN||cos 〈MN,n〉|=.(2)利用空间向量求空间距离问题,首先应明确所求距离的特征,恰当选用距离公式求解. 1.如图,PABCD 是正四棱锥,ABCDA1B1C1D1是正方体,其中 AB=2,PA=,则 B1到平面PAD 的距离为________.解析:以 A1为原点,以 A1B1所在直线为 x 轴,A1D1所在直线为 y 轴,A1A 所在直线为 z 轴建立空间直角坐标系 A1xyz,则AD=(0,2,0),AP=(1,1,2),设平面 PAD 的法向量是 m=(x,y,z),所以由可得取 z=1,得 m=(-2,0,1),因为B1A=(-2,0,2),所以 B1到平面 PAD 的距离 d==.答案:2.如图,在长方体 ABCDA1B1C1D1中,AB=4,BC=3,CC1=2.(1)求证:平面 A1BC1∥平面 ACD1;(2)求平面 A1BC1与平面 ACD1的距离.解:(1)证明:因为 AA1綊 CC1,所以四边形 ACC1A1为平行四边形,所以 AC∥A1C1.又 AC⊄平面 A1BC1,A1C1⊂平面 A1B...