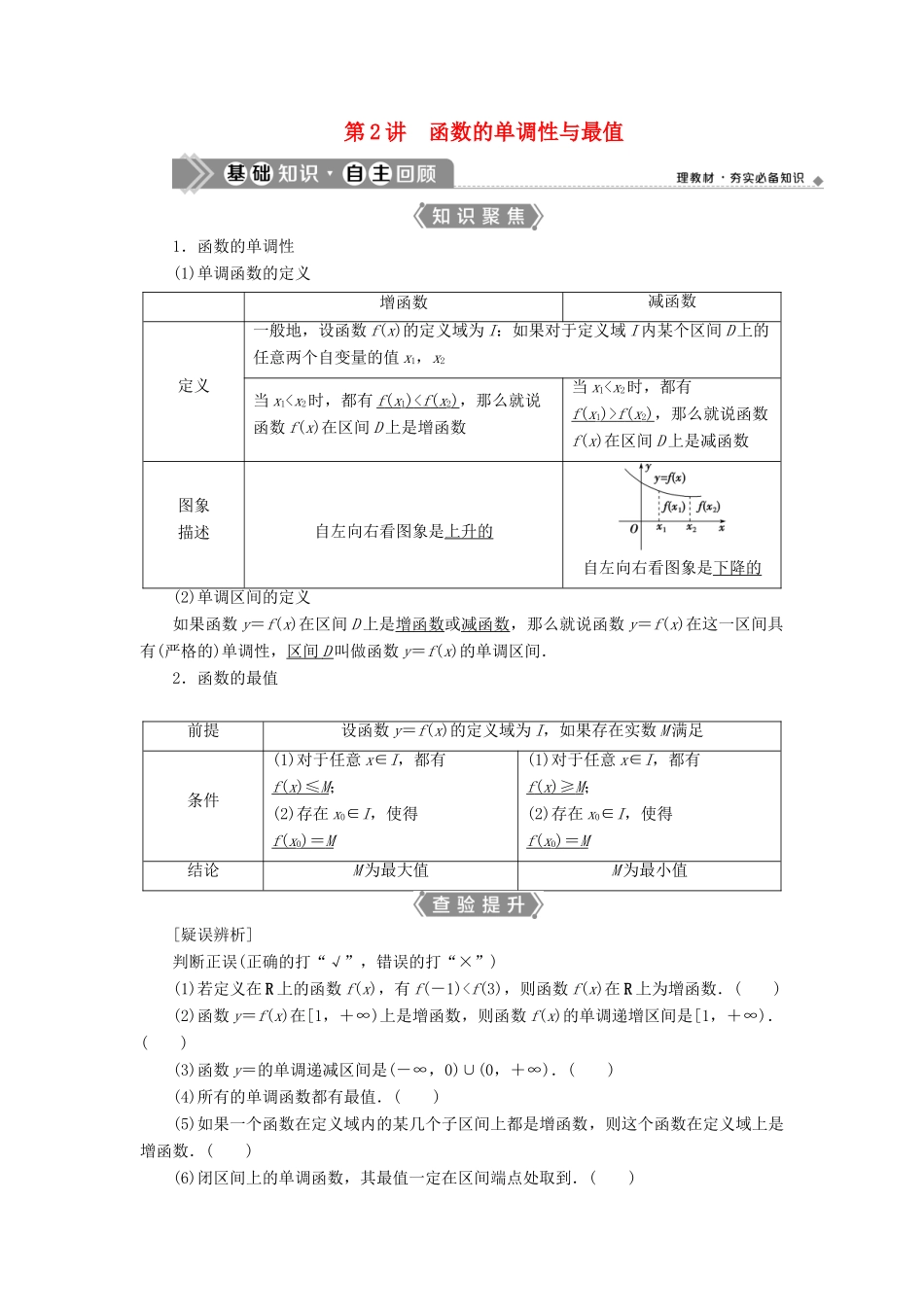
第 2 讲 函数的单调性与最值1.函数的单调性(1)单调函数的定义增函数减函数定义一般地,设函数 f(x)的定义域为 I:如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x1,x2当 x1 f ( x 2),那么就说函数f(x)在区间 D 上是减函数图象描述自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数 y=f(x)在区间 D 上是增函数或减函数,那么就说函数 y=f(x)在这一区间具有(严格的)单调性,区间 D 叫做函数 y=f(x)的单调区间.2.函数的最值前提设函数 y=f(x)的定义域为 I,如果存在实数 M 满足条件(1)对于任意 x∈I,都有f ( x )≤ M ;(2)存在 x0∈I,使得f ( x 0) = M (1)对于任意 x∈I,都有f ( x )≥ M ;(2)存在 x0∈I,使得f ( x 0) = M 结论M 为最大值M 为最小值[疑误辨析]判断正误(正确的打“√”,错误的打“×”)(1)若定义在 R 上的函数 f(x),有 f(-1)