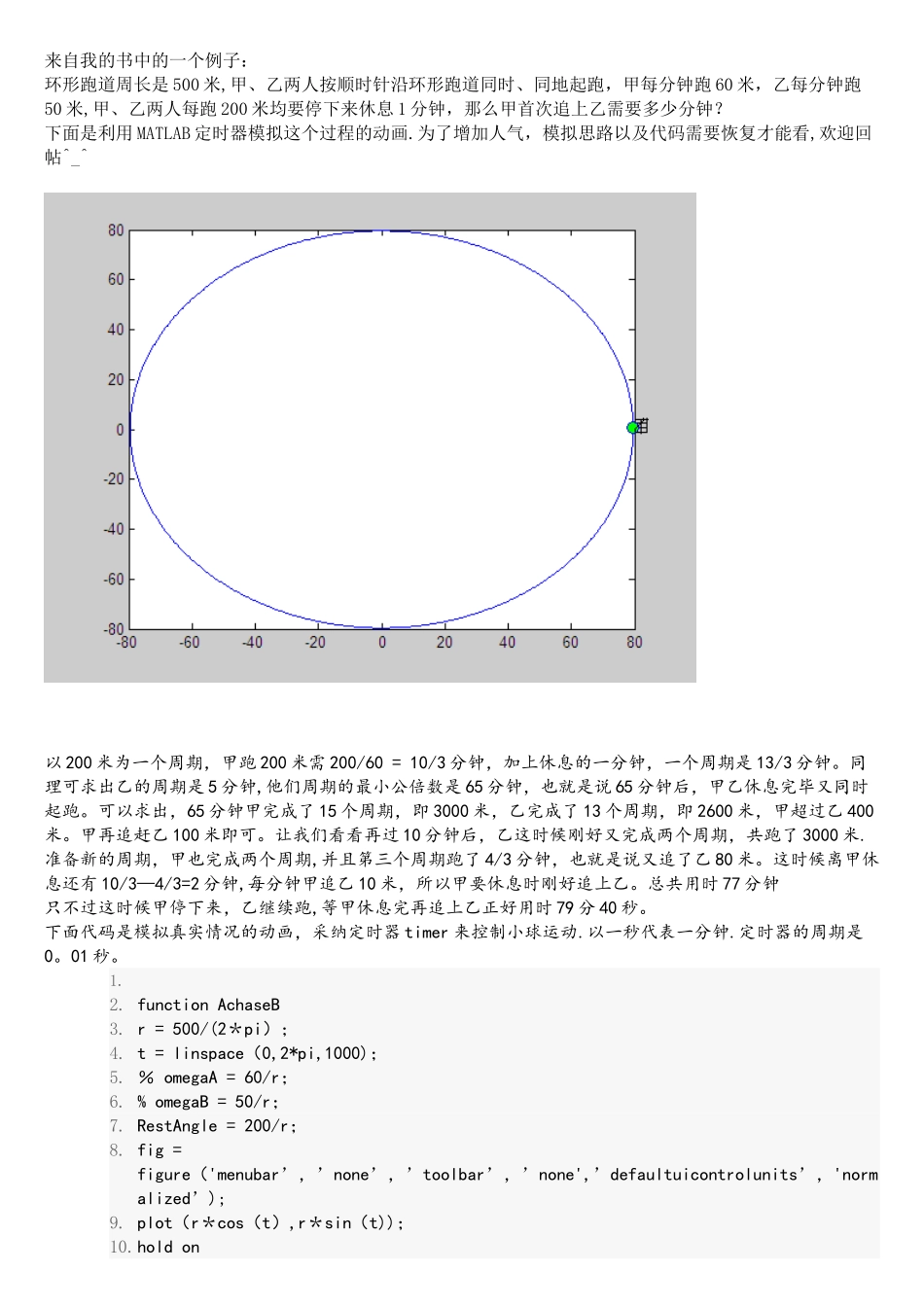
来自我的书中的一个例子:环形跑道周长是 500 米,甲、乙两人按顺时针沿环形跑道同时、同地起跑,甲每分钟跑 60 米,乙每分钟跑50 米,甲、乙两人每跑 200 米均要停下来休息 1 分钟,那么甲首次追上乙需要多少分钟?下面是利用 MATLAB 定时器模拟这个过程的动画.为了增加人气,模拟思路以及代码需要恢复才能看,欢迎回帖^_^以 200 米为一个周期,甲跑 200 米需 200/60 = 10/3 分钟,加上休息的一分钟,一个周期是 13/3 分钟。同理可求出乙的周期是 5 分钟,他们周期的最小公倍数是 65 分钟,也就是说 65 分钟后,甲乙休息完毕又同时起跑。可以求出,65 分钟甲完成了 15 个周期,即 3000 米,乙完成了 13 个周期,即 2600 米,甲超过乙 400米。甲再追赶乙 100 米即可。让我们看看再过 10 分钟后,乙这时候刚好又完成两个周期,共跑了 3000 米.准备新的周期,甲也完成两个周期,并且第三个周期跑了 4/3 分钟,也就是说又追了乙 80 米。这时候离甲休息还有 10/3—4/3=2 分钟,每分钟甲追乙 10 米,所以甲要休息时刚好追上乙。总共用时 77 分钟只不过这时候甲停下来,乙继续跑,等甲休息完再追上乙正好用时 79 分 40 秒。 下面代码是模拟真实情况的动画,采纳定时器 timer 来控制小球运动.以一秒代表一分钟.定时器的周期是0。01 秒。 1.2. function AchaseB3. r = 500/(2*pi);4. t = linspace(0,2*pi,1000);5. % omegaA = 60/r;6. % omegaB = 50/r;7. RestAngle = 200/r;8. fig = figure('menubar’,’none’,’toolbar’,’none',’defaultuicontrolunits’,'normalized’);9. plot(r*cos(t),r*sin(t));10.hold on11.A = plot(r*cos(0),r*sin(0),'marker','o',’MarkerSize’,8,’MarkerFaceColor’,'r’);12.aa = text(r*cos(0),r*sin(0),'甲');13.B = plot(r*cos(0),r*sin(0),'marker’,'o’,’MarkerSize',8,'MarkerFaceColor’,’g');14.bb = text(r*cos(0),r*sin(0),'乙');15.timerA = timer(’TimerFcn’,@TimerFcnA,’executionmode’,'fixedspacing','period',0。01);16.timerB = timer('TimerFcn’,@TimerFcnB,'executionmode’,'fixedspacing’,’period’,0。01);17.start(timerA);start(timerB);18.%%19. function TimerFcnA(timerA,event)20. nA = get(timerA,'TasksExecute...