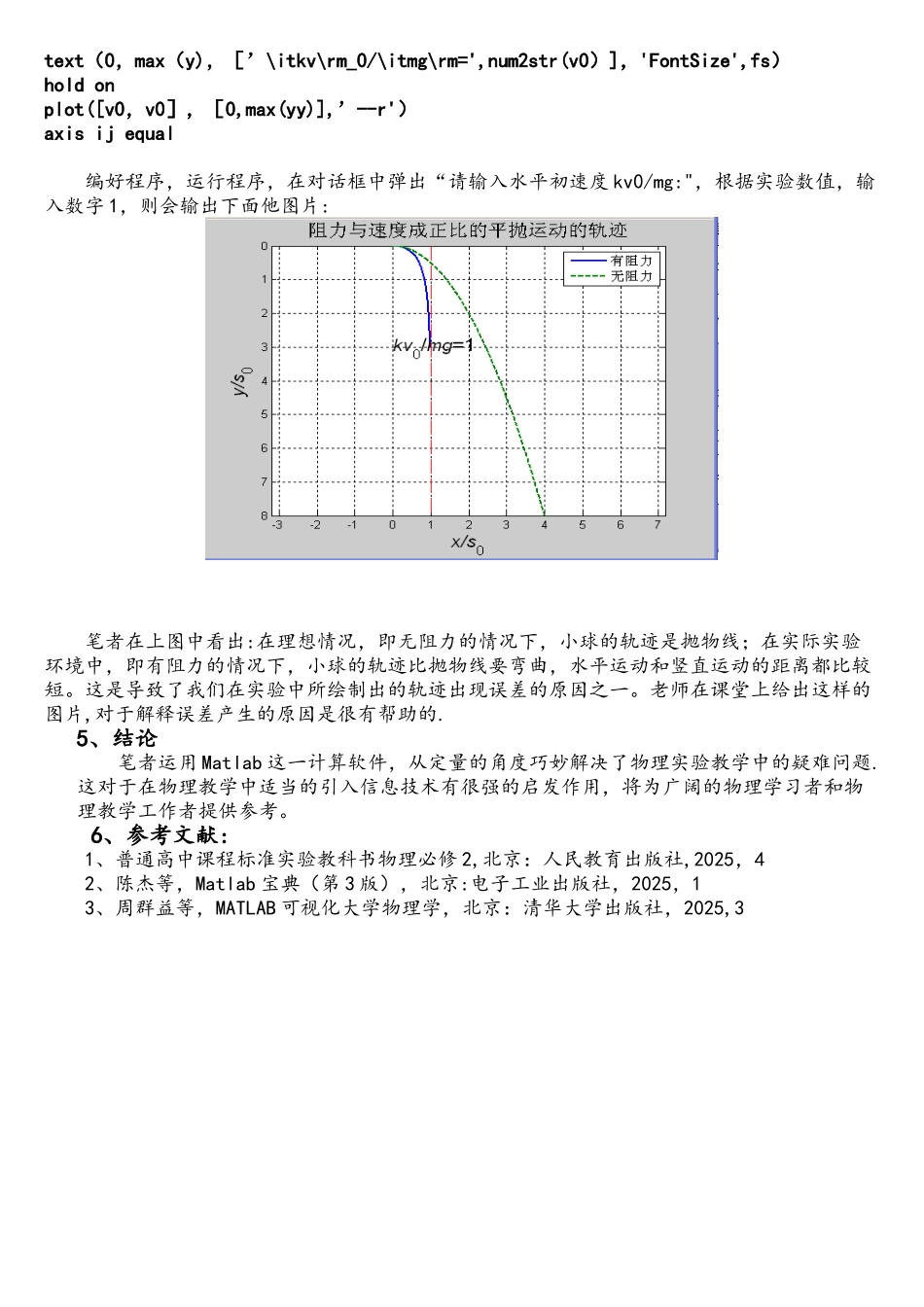
利用 Matlab 软件分析空气中做平抛运动小球的轨迹摘要:分析在做平抛实验中物体实际运行的轨迹与理论轨迹出现差异的原因,并通过计算推导,借助 Matlab软件将这种差异表征出来关键词:Matlab,轨迹1、问题引出 在人民教育出版社高中物理必修 2 的第五章曲线运动第 3 节实验课:讨论平抛运动中,在第14 页参考案例一中,有这样的叙述:“钢球从斜槽上滚下,重钢水平槽飞出后做平抛运动,每次都使钢球在斜槽上同一位置滚下,钢球在空中做平抛运动的轨迹就是一定的。设法用铅笔妙处小球经过的位置.通过多次试验,在竖直白纸上记录钢球所经过的多个位置,连起来就得到钢球做平抛运动的轨迹”.细心的同学在做实验时发现钢球运动的轨迹与理论轨迹有差别,一般的解释是由于空气阻力的影响。但空气阻力是如何影响运动轨迹的?空气阻力对运动轨迹的影响有多大?这方面的讨论鲜有所见,为此,笔者实行信息技术对这一问题进行探讨.2、Matlab 简介 Matlab 是 Mathworks 公司推出的一套高性能数值计算和可视化软件,它集数值分析、矩阵运算、信号处理和图形显示于一体,在系统建模和仿真、科学和工程绘图及应用程序开发等方面有着广泛应用,Matlab 已经由简单的矩阵计算软件分析进展成为通用性极高、带有多种有用工具的运算操作平台.3、方程推导假设一小钢球在空气中做平抛运动,初速度为 v0,所受的阻力与速率成正比:f = —kv,k称为阻力系数。在此实验中,小球的质量 m=0.1kg,初速度 V0=2m/s,空气阻力系数 k=0.5。如图所示,小球受到重力 mg,方向竖直向下;空气阻力 f,方向与速度方向相反。根据牛顿第二定律可列出直角坐标方程由于 Vx = dx/dt,Vy = dy/dt,上式可化为分离变量得mgxOfy积分得当 t = 0 时,Vx = V0,Vy = 0,可得 Cx = —V0,Cy = -g,因此当 t = 0 时,x = 0,y = 0,积分上式可得 这是小球的运动方程,也是以时间 t 为参数的轨道方程。在此实验中,小球的质量m=0.1kg,初速度 V0=2m/s,空气阻力系数 k=0.5。所以实验中的小球的运动方程可表示为: 4、编程与绘图在 matlab 软件中,调用 edit 编辑器,编写程序如下:clear t=0:0.01:4; v0=input(’请输入水平初速度kv0/mg:’); x=v0*(1-exp(-t)); y=t+exp(—t)—1; xx=v0*t; yy=t。^2/2; fs=16; text(0,max(y),[’\itkv\rm_0/\itmg\rm=’,num2str(v0)],'FontSize',fs)figure plot(x,y,xx,yy,’—-','LineWidth...