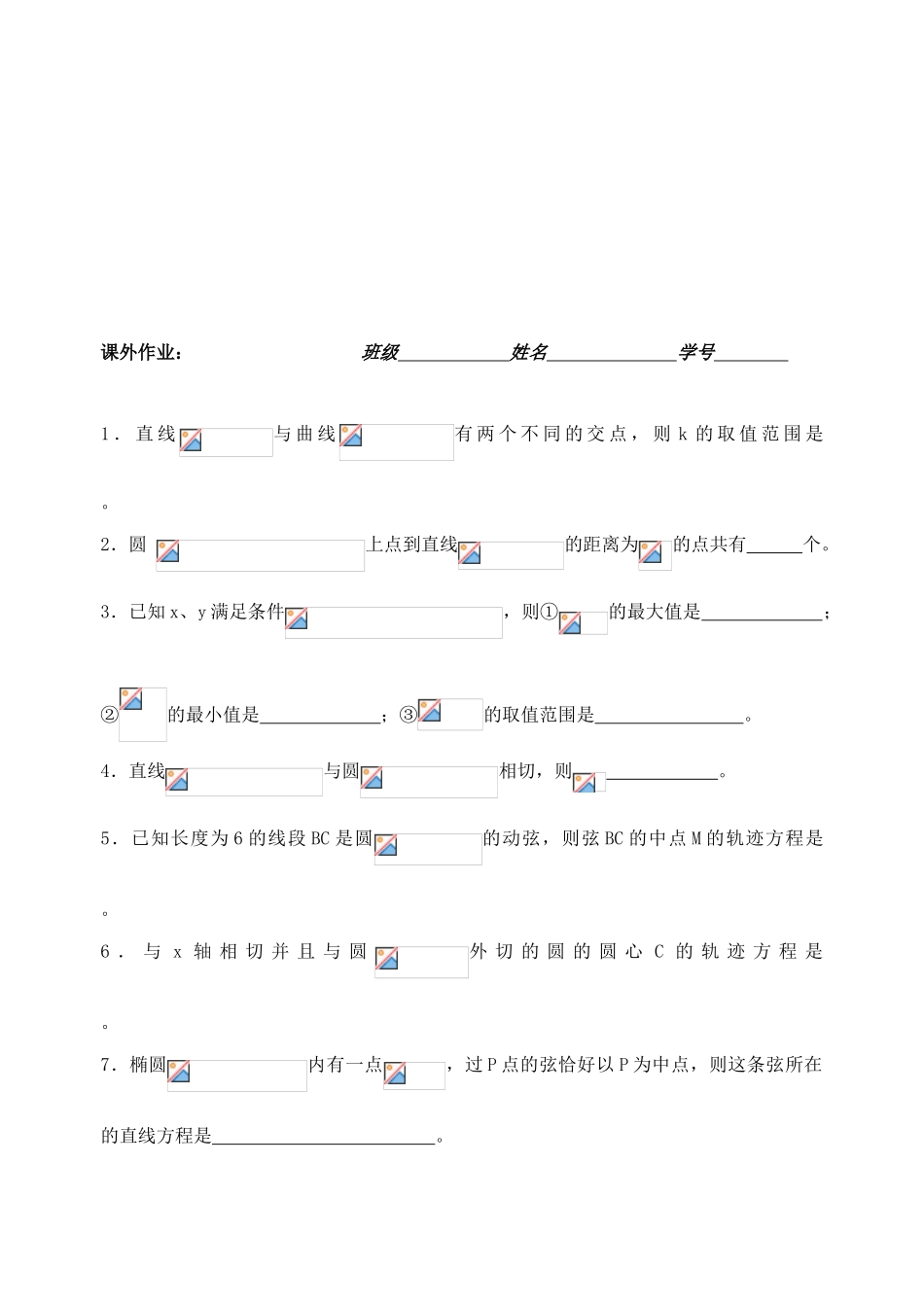
圆锥曲线复习(学案) ——直线与圆、椭圆的关系复习目标:(1)判断直线与圆、直线与椭圆的位置关系; (2)求解直线与圆、直线与椭圆的弦的问题; (3)数形结合法、分类讨论法、“点差法”以及函数思想方法等。复习重点:直线与圆、直线与椭圆的弦的问题基础训练:1.直线被圆截得的弦长是 。2.由点向圆引切线,则切线长为 。3.以为圆心,且与圆内切的圆的方程是 。4.椭圆上一点 P 到焦点的距离为 2,M 为线段的中点,O 为原点,则 。5.椭圆的一个顶点和一个焦点在直线上,则此椭圆的标准方程是 。例题精讲:例题 1 直线与椭圆交于 M、N 两点,求过 M、N 两点且与直线相切的圆的方程。例 题 2 求 与 已 知 圆相 交 , 所 得 公 共 弦 所 在 直 线 方 程 为,且过点的圆的方程。例题 3 过点作直线与椭圆交于 A、B 两点,O 为原点,求△AOB 面积的最大值。例题 4 设为椭圆 C1:的左焦点,M 是椭圆 C1上任意一点,P 是线段的中点。(1)求动点 P 的轨迹 C 方程;(2)若直线交轨迹 C 于 A、B 两点,AB 的中垂线交 y 轴于,求 t 的取值范围。课外作业: 班级 姓名 学号 1 . 直 线与 曲 线有 两 个 不 同 的 交 点 , 则 k 的 取 值 范 围 是 。2.圆 上点到直线的距离为的点共有 个。3.已知 x、y 满足条件,则①的最大值是 ;②的最小值是 ;③的取值范围是 。4.直线与圆相切,则 。5.已知长度为 6 的线段 BC 是圆的动弦,则弦 BC 的中点 M 的轨迹方程是 。6 . 与 x 轴 相 切 并 且 与 圆外 切 的 圆 的 圆 心 C 的 轨 迹 方 程 是 。7.椭圆内有一点,过 P 点的弦恰好以 P 为中点,则这条弦所在的直线方程是 。8.已知椭圆的中心在原点,焦点在 x 轴上,右焦点到直线的距离为 3,一个顶点坐标为,则求椭圆的方程是 。9.已知直线与椭圆有两个不同的交点,则 m 的取值范围是 。10.若直线与圆没有公共点,则 m、n 满足的关系是为 ; 以为 点 P 的 坐 标 , 过 P 的 一 条 直 线 与 椭 圆的 公 共 点 有 个。11.已知椭圆 C 的焦点分别为、,长轴长是短轴长的 2 倍。(1)求椭圆上点到直线的距离的最大值;(2)若 P 在椭圆上,,求△的面积。12 . 椭 圆 C :的 两 个 焦 点 为、, 点 P 在 椭 圆 C 上 , 且,,。 ( 1 ) 求 椭 圆 C 的 方 程 ; ( 2 ) 若 直 线 l 过 圆的圆心 M,交椭圆 C 于 A、B 两点,且 A、B 关于点 M 对称,求直线 l的方程。