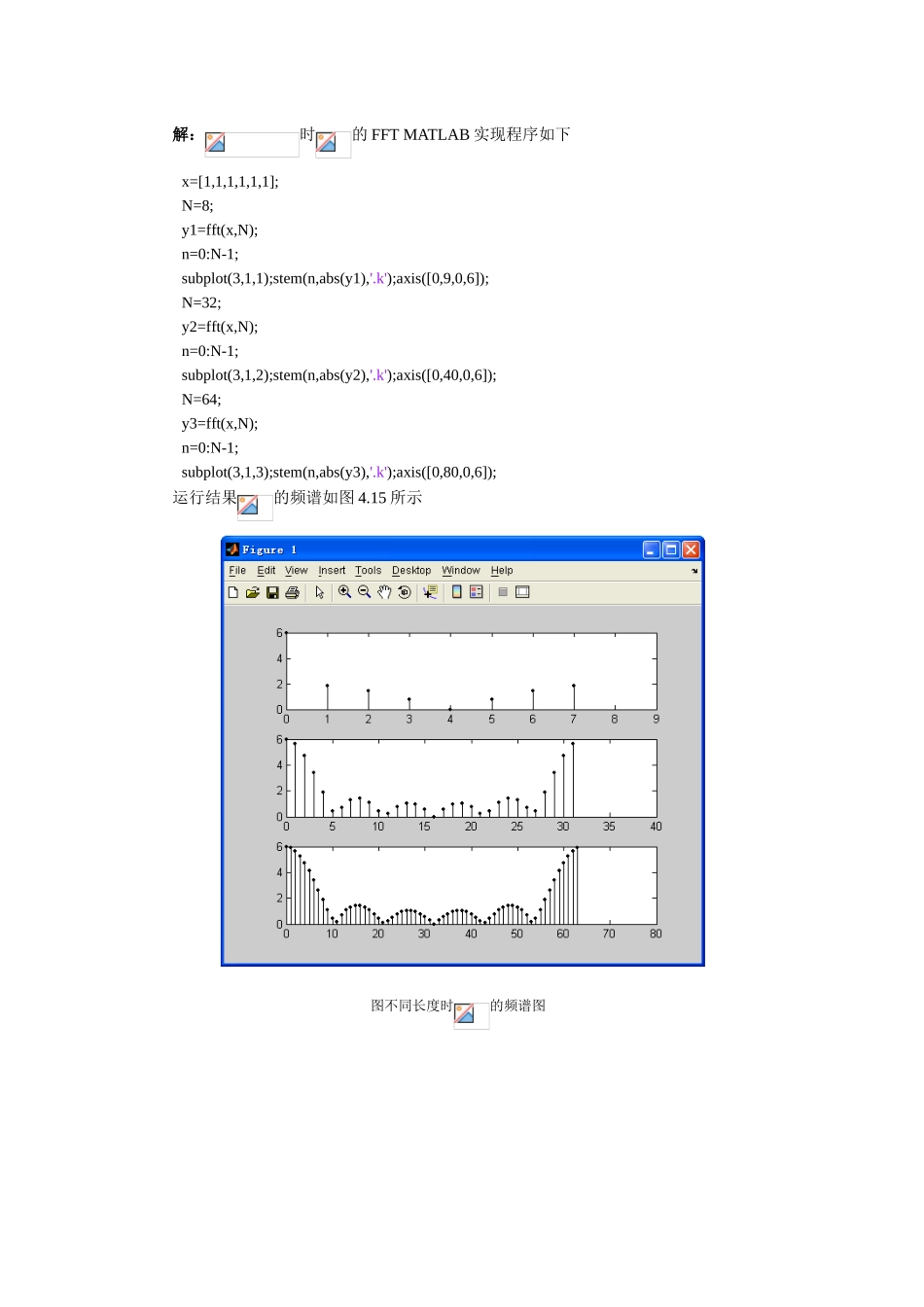
实验二 用 DFT 及 FFT 进行谱分析 (2 学时)1.目的要求 进一步加深 DFT 算法原理和基本性质的理解;熟悉 FFT 算法原理和 FFT 子程序的应用;学习用 FFT 对连续信号和时域离散信号进行谱分析的方法,以便在实际中正确应用 FFT。2.方法原理 参考《数字信号处理》教材的快速傅立叶变换一章。3.主要实验仪器及材料微型计算机、Matlab6.5 教学版、TC 编程环境。4.掌握要点结合实验中获得的序列幅频特性曲线,分析所得的图形,说明用 FFT 作谱分析时有关参数的选择方法。5.实验内容(1)用 Matlab 或 C 语言编制信号产生子程序, 产生典型信号供谱分析用;例如 1:(1)产生一个三角波序列,长度为 M=40;(2)计算 N=64 时的,并图示和;(3)对在[0,2π]上进行 32 点抽样,得到,k=0,1,…,31(4)求的 32 点 IDFT,即(5)绘制的波形图,观察和的关系,并加以说明。2 设为长度的矩形序列,用 MATLAB 程序分析 FFT 取不同长度时的频谱变化。(2)画对给出信号逐个进行谱分析,绘出序列和幅频特性曲线;(3)设计利用快速傅里叶变换 FFT 计算序列频谱程序;(4)对结果进行分析;(5)完成实验报告。解:时的 FFT MATLAB 实现程序如下x=[1,1,1,1,1,1];N=8;y1=fft(x,N);n=0:N-1;subplot(3,1,1);stem(n,abs(y1),'.k');axis([0,9,0,6]);N=32;y2=fft(x,N);n=0:N-1;subplot(3,1,2);stem(n,abs(y2),'.k');axis([0,40,0,6]);N=64;y3=fft(x,N);n=0:N-1;subplot(3,1,3);stem(n,abs(y3),'.k');axis([0,80,0,6]);运行结果的频谱如图 4.15 所示图不同长度时的频谱图