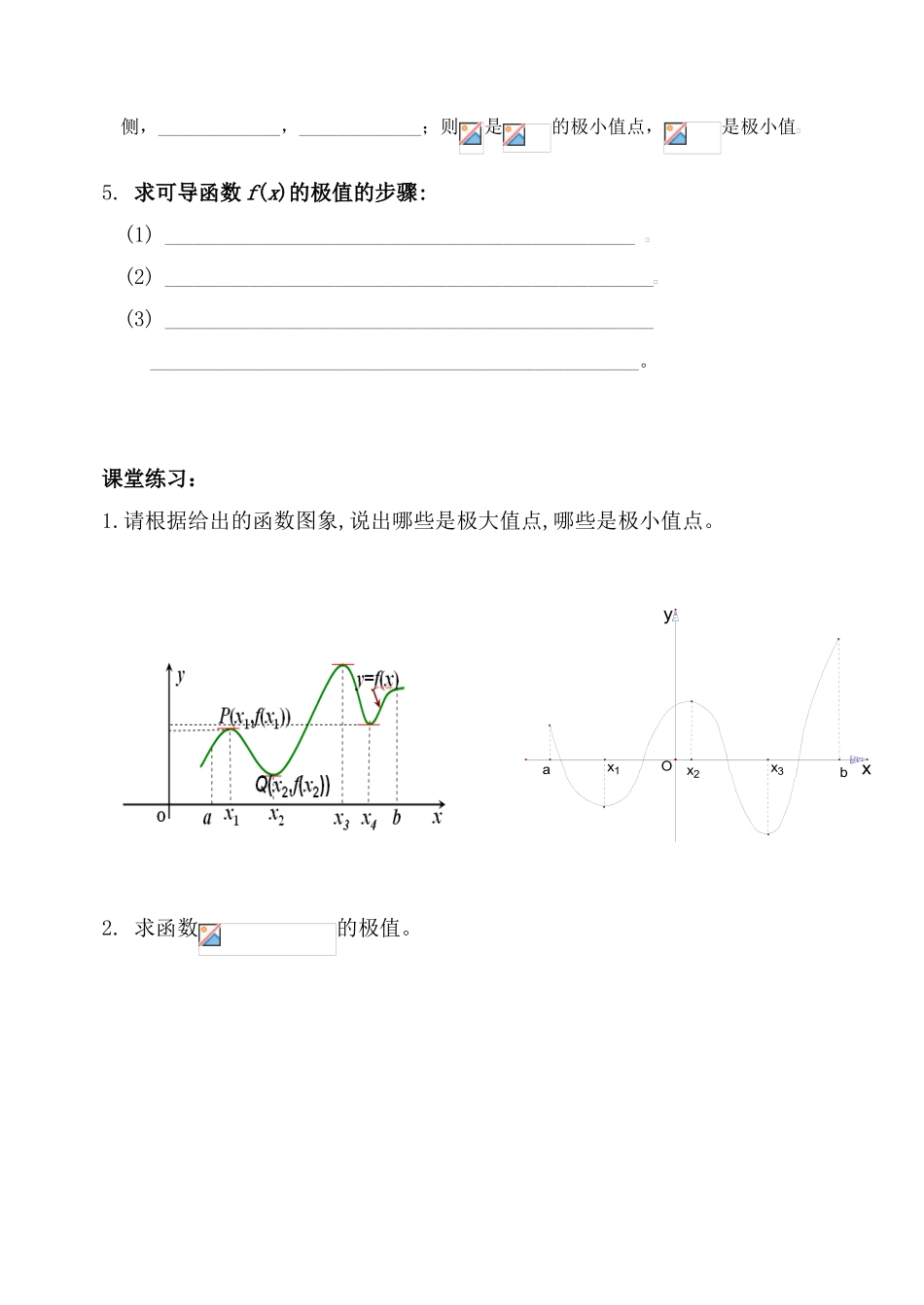
1.3.2 利用导数研究函数的极值学习目标:了解函数在某点取得极值的条件;会用导数求函数的极大值、极小值;会求闭区间上函数的最大值、最小值。知识回顾:函数的导数与函数的单调性的关系:设函数 y=f(x) 在某个区间内有导数,如果在这个区间内>0,那么函数 y=f(x) 在这个区间上_____________如果在这个区间内<0,那么函数 y=f(x) 在这个区间上_____________新课探究:1. 极大值: 一般地,设函数 f(x)在点 x0附近有定义,如果对 x0附近的所有的点,都有_____________,就说 f(x0)是函数 f(x)的一个极大值,记作__________________________._____________是极大值点2. 极小值:一般地,设函数 f(x)在 x0附近有定义,如果对 x0附近的所有的点,都有_____________.就说 f(x0)是函数 f(x)的一个极小值,记作__________________________,_____________是极小值点3. 极大值与极小值统称为_____________4. 判别 f(x0)是极大、极小值的方法:若满足,在的左侧,_____________,_____________;在的右侧,_____________,_____________;则是的极大值点,是极大值若满足,在的左侧,_____________,_____________;在的右侧,_____________,_____________;则是的极小值点,是极小值5. 求可导函数 f(x)的极值的步骤:(1) __________________________________________________ (2) ____________________________________________________(3) ________________________________________________________________________________________________________。课堂练习:1.请根据给出的函数图象,说出哪些是极大值点,哪些是极小值点。2. 求函数的极值。x3x2x1baxOy3. 已知函数,求函数的极值,并画出函数的大致图像。4. 已知函数,求函数在区间[ - 3,4]上的最大值和最小值。求函数在区间[ - 3,5]上的最大值和最小值。设函数在上连续,在内可导,则求在的最大值与最小值的步骤如下:(1)_____________________________________________(2)__________________________________________________________________________________________活学活用1. 求函数 f(x)=在区间[1,5]内的最大值和最小值 .2. 函数在时取得极值,求 a 的值。3. 求函数在区间上的最大值与最小值思维导图导数的应用