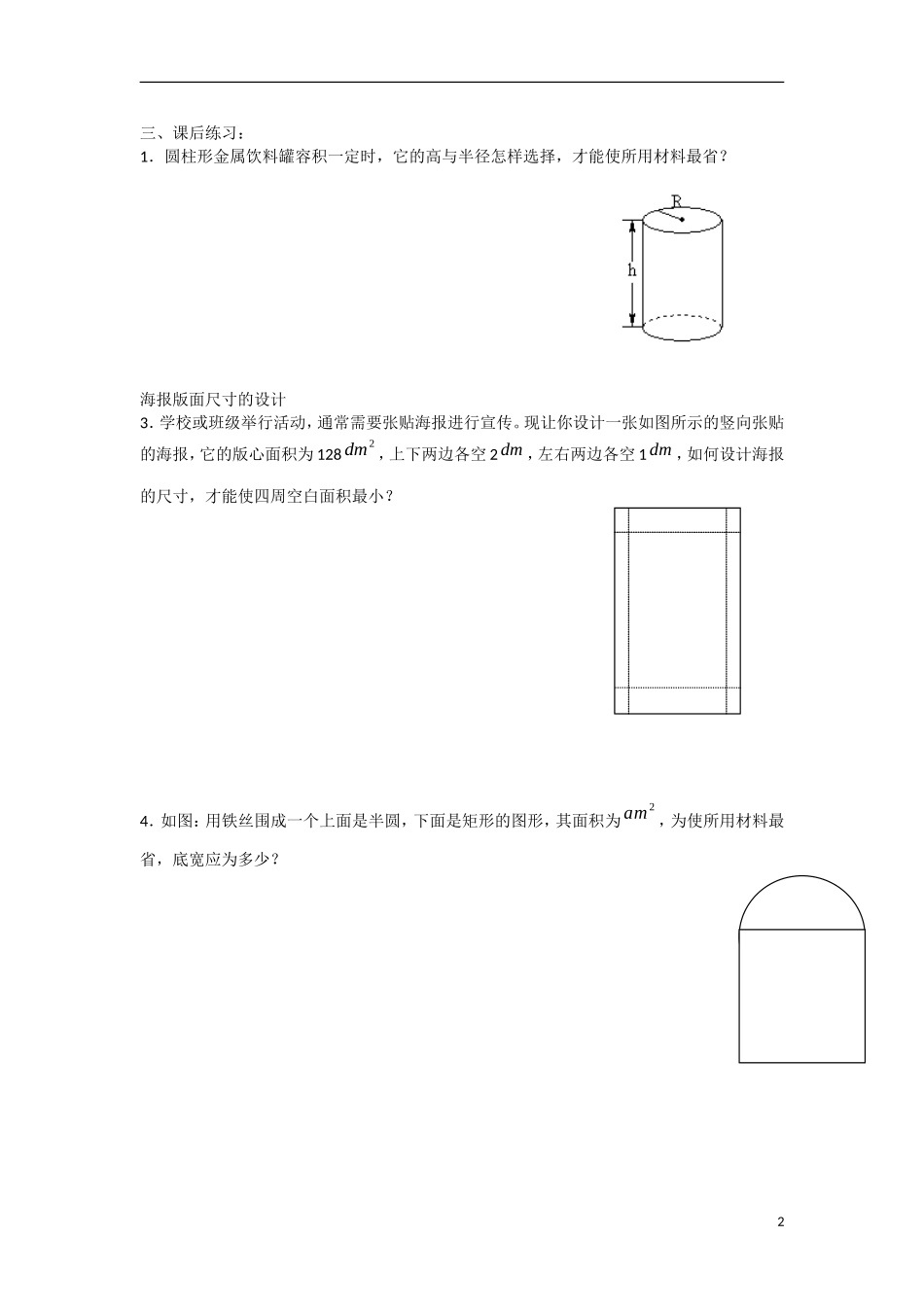
1.3.3 导数的实际应用【教学目标】利用导数解决实际问题中的最优化问题,掌握建立数学模型的方法,形成求解优化问题的思路和方法.【教学重点】实际问题中的导数应用 【教学难点】数学建模 一、课前预习:1.利用导数求函数极值和最值的方法:2.自主学习教材 31 页例 1、例 2,总结利用导数解决生活中的优化问题的一般步骤:例 1 有一块边长为 a 的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方形的无盖容器,为使其容积最大,截下的小正方形的边长应为多少?例 2 横截面为矩形的横梁的强度同它的断面的高的平方与宽的积成正比,要将直径为 d 的圆木锯成强度最大的横梁,断面的宽度和高度应是多少?利用导数解决生活中的优化问题的一般步骤:(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系)(xfy ;(2)求函数的导数)(/ xf,解方程0)(/xf;(3)比较函数在区间端点和使0)(/xf的点的函数值的大小,最大(小)者为最大(小)值。二、课上学习:1.已知某厂生产 x 件产品的成本为240120025000xxc(元)。(1)要使平均成本最低,应生产多少件产品?(2)若产品以每件 500 元售出,要使利润最大,应生产多少件产品?1三、课后练习:1.圆柱形金属饮料罐容积一定时,它的高与半径怎样选择,才能使所用材料最省?海报版面尺寸的设计3.学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图所示的竖向张贴的海报,它的版心面积为 1282dm ,上下两边各空 2 dm ,左右两边各空 1 dm ,如何设计海报的尺寸,才能使四周空白面积最小?4.如图:用铁丝围成一个上面是半圆,下面是矩形的图形,其面积为2ma,为使所用材料最省,底宽应为多少?2xyO-212xyO-212高考连接:1. ( 2012 年 高 考 ( 重 庆 理 ) ) 设 函 数( )f x 在 R 上 可 导 , 其 导 函 数 为( )fx, 且 函 数(1)( )yx fx 的图像如图所示,则下列结论中一定成立的是A.函数( )f x 有极大值(2)f和极小值(1)f B.函数( )f x 有极大值( 2)f 和极小值(1)f C.函数( )f x 有极大值(2)f和极小值( 2)f D.函数( )f x 有极大值( 2)f 和极小值(2)f2.(2012 年高考(陕西理))设函数( )xf xxe,则A.1x 为( )f x 的极大值点B.1x 为( )f x 的极小值点 C.1x 为( )f x 的...