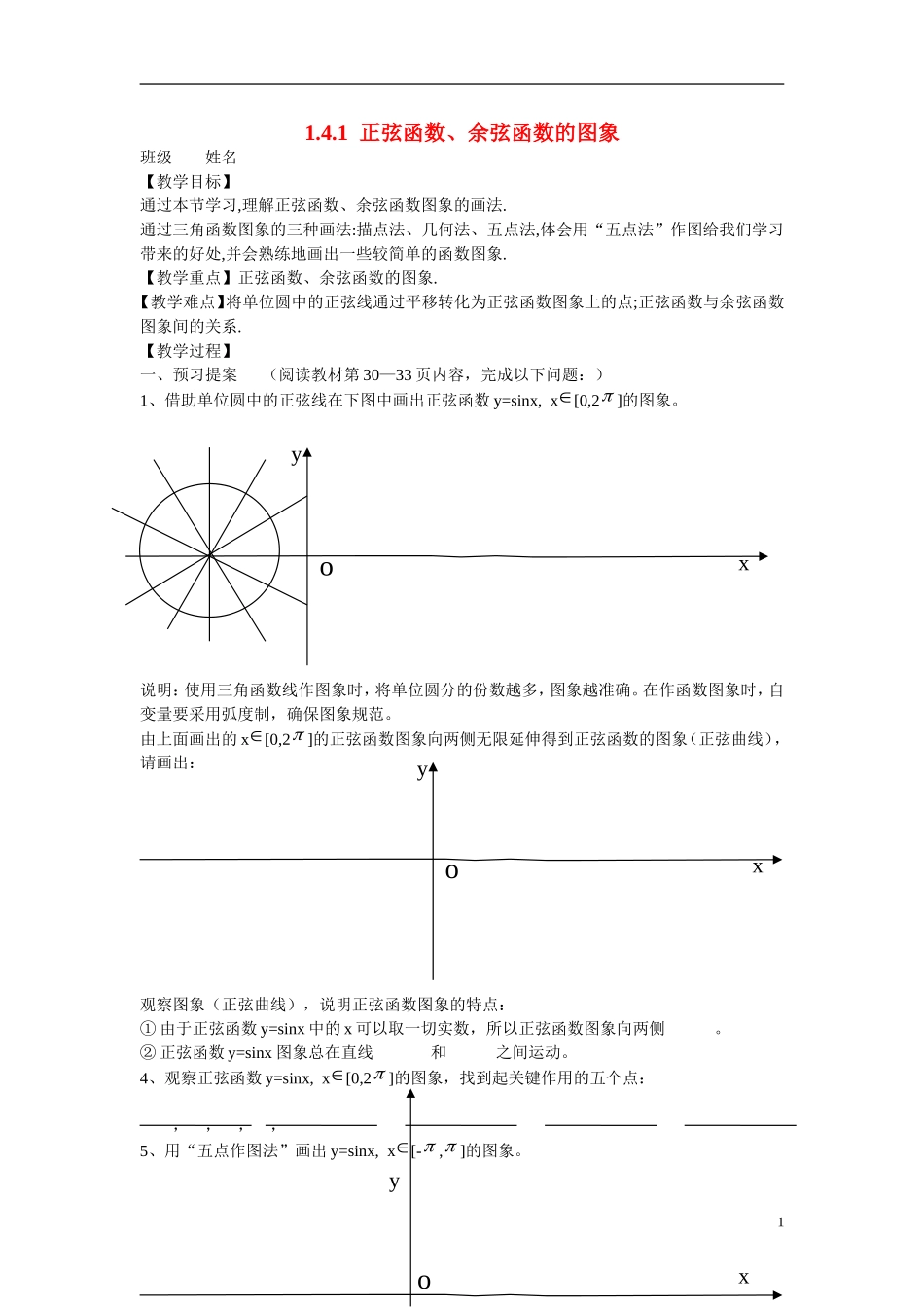
1.4.1 正弦函数、余弦函数的图象班级 姓名 【教学目标】通过本节学习,理解正弦函数、余弦函数图象的画法.通过三角函数图象的三种画法:描点法、几何法、五点法,体会用“五点法”作图给我们学习带来的好处,并会熟练地画出一些较简单的函数图象.【教学重点】正弦函数、余弦函数的图象.【教学难点】将单位圆中的正弦线通过平移转化为正弦函数图象上的点;正弦函数与余弦函数图象间的关系.【教学过程】一、预习提案 (阅读教材第 30—33 页内容,完成以下问题:)1、借助单位圆中的正弦线在下图中画出正弦函数 y=sinx, x[0,2 ]的图象。 说明:使用三角函数线作图象时,将单位圆分的份数越多,图象越准确。在作函数图象时,自变量要采用弧度制,确保图象规范。由上面画出的 x[0,2 ]的正弦函数图象向两侧无限延伸得到正弦函数的图象(正弦曲线),请画出:观察图象(正弦曲线),说明正弦函数图象的特点:① 由于正弦函数 y=sinx 中的 x 可以取一切实数,所以正弦函数图象向两侧 。② 正弦函数 y=sinx 图象总在直线 和 之间运动。4、观察正弦函数 y=sinx, x[0,2 ]的图象,找到起关键作用的五个点:,,,,5、用“五点作图法”画出 y=sinx, x[- , ]的图象。1oyxoxyoyx6、①函数 ƒ(x+1)的图象相对于函数 ƒ(x)的图象是如何变化的?② 函数 y=sin(x+ 2)的图象相对于正弦函数 y=sinx 的图象是如何变化的?③ 由诱导公式知:sin(x+ 2)= ,所以函数 y=sin(x+ 2)=④ 请画出 y=cosx 的图象(余弦曲线)7、观察余弦函数 y=cosx, x[0,2 ]的图象,找到起关键作用的五个点:,,,,8、用“五点作图法”画出 y=cosx, x[- , ]的图象。二、新课讲解例 1、用“五点作图法”作出 y=xsin, x[0,2 ]的图象;并通过猜想画出 y=xsin在整个定义域内的图象。2oxyoxy练习:用“五点作图法”作出 y=xcos, x[0,2 ]的图象;并通过猜想画出 y=xcos在整个定义域内的图象。例 2、用“五点作图法”作出下列函数的简图;(1)y=1+sinx, x[0,2 ];(2)y=2cos(2x- 3) 3练习:用“五点作图法”作出下列函数的简图;(1)y=-cosx, x[0,2 ];(2)y=2sin(x- 3)+1三、课堂小结 1、 会用“五点法”作图熟练地画出一些较简单的函数图象. 2、关键点是指图象的最高点,最低点及与 x 轴的交点。四、作业布置 习题 1.4 A 组第 1 题4