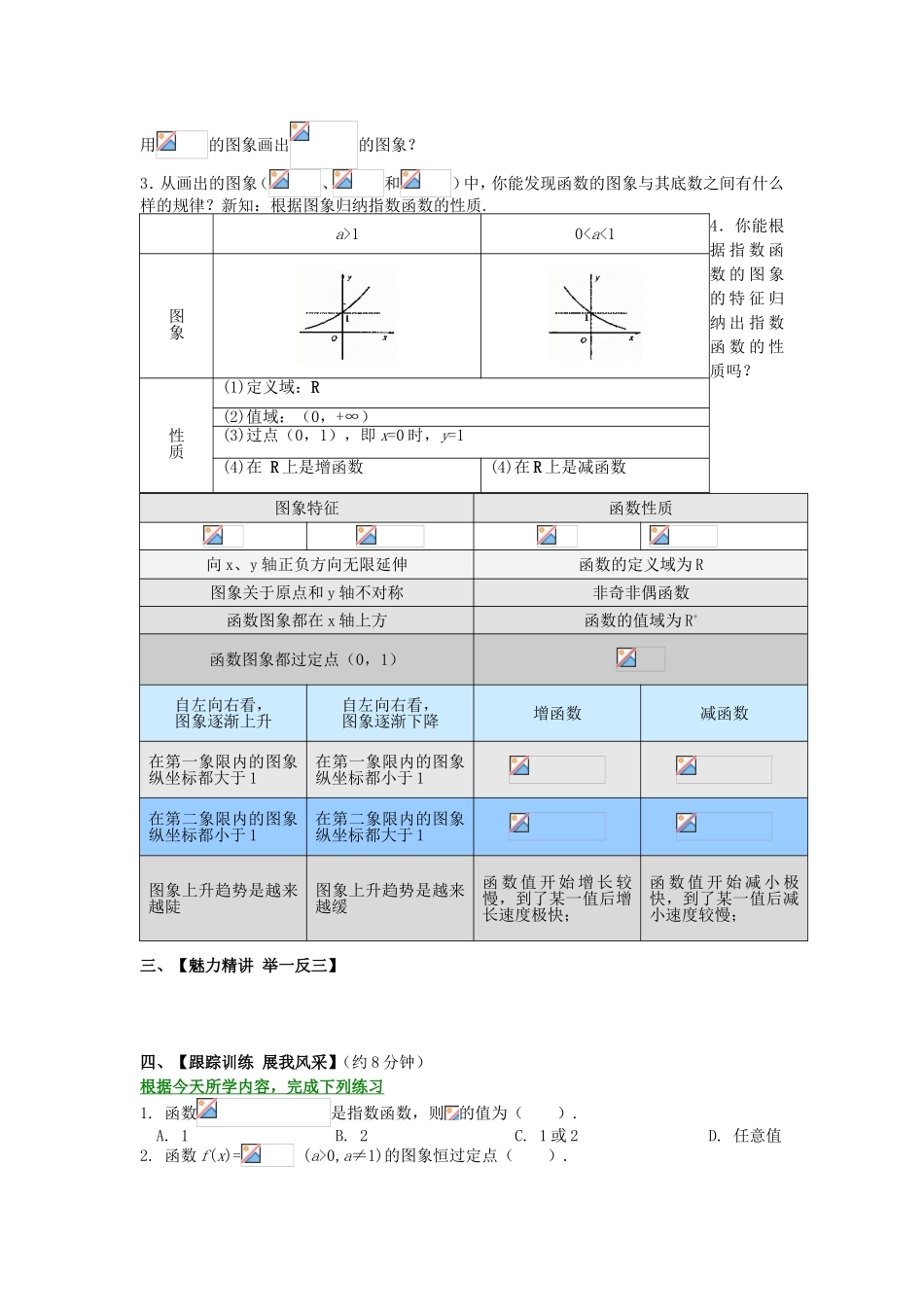
2.1.2 指数函数及其性质一、【学习目标】1. 了解指数函数模型的实际背景,认识数学与现实生活及其他学科的联系;2. 理解指数函数的概念和意义;3. 能画出具体指数函数的图象,掌握指数函数的性质(单调性、特殊点).二、【自学内容和要求及自学过程】课前准备复习 1:零指数、负指数、分数指数幂怎样定义的?(1) ;(2) ;(3) ; .其中复习 2:有理指数幂的运算性质.(1) ;(2) ;(3) .新课导学探究任务一:指数函数模型思想及指数函数概念实例: A.细胞分裂时,第一次由 1 个分裂成 2 个,第 2 次由 2 个分裂成 4 个,第 3 次由 4 个分裂成8 个,如此下去,如果第 x 次分裂得到 y 个细胞,那么细胞个数 y 与次数 x 的函数关系式是什么? B.一种放射性物质不断变化成其他物质,每经过一年的残留量是原来的 84%,那么以时间x 年为自变量,残留量 y 的函数关系式是什么?讨论:上面的两个函数有什么共同特征?底数是什么?指数是什么?新知:一般地,函数叫做指数函数(exponential function),其中 x是自变量,函数的定义域为 R.注意: 指数函数的定义是一个形式定义,要引导学生辨析; 注意指数函数的底数的取值范围,引导学生分析底数为什么不能是负数、零和 1.反思:为什么规定>0 且≠1 呢?否则会出现什么情况呢?探究任务二:指数函数的图象和性质问题:你能类比前面讨论函数性质时的思路,提出研究指数函数性质的内容和方法吗?研究方法:画出函数的图象,结合图象研究函数的性质.研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.1.在同一坐标系中画出下列函数的图象:(1)(2)(3)(4)(5)2.从画出的图象中你能发现函数的图象和函数的图象有什么关系?可否利用的图象画出的图象?3.从画出的图象(、和)中,你能发现函数的图象与其底数之间有什么样的规律?新知:根据图象归纳指数函数的性质.4.你能根据 指 数 函数 的 图 象的 特 征 归纳 出 指 数函 数 的 性质吗?三、【魅力精讲 举一反三】四、【跟踪训练 展我风采】(约 8 分钟)根据今天所学内容,完成下列练习1. 函数是指数函数,则的值为( ). A. 1 B. 2 C. 1 或 2 D. 任意值2. 函数 f(x)= (a>0,a≠1)的图象恒过定点( ).a>10