高中数学 2.2 等差数列的前n项和学案 北师大版必修5

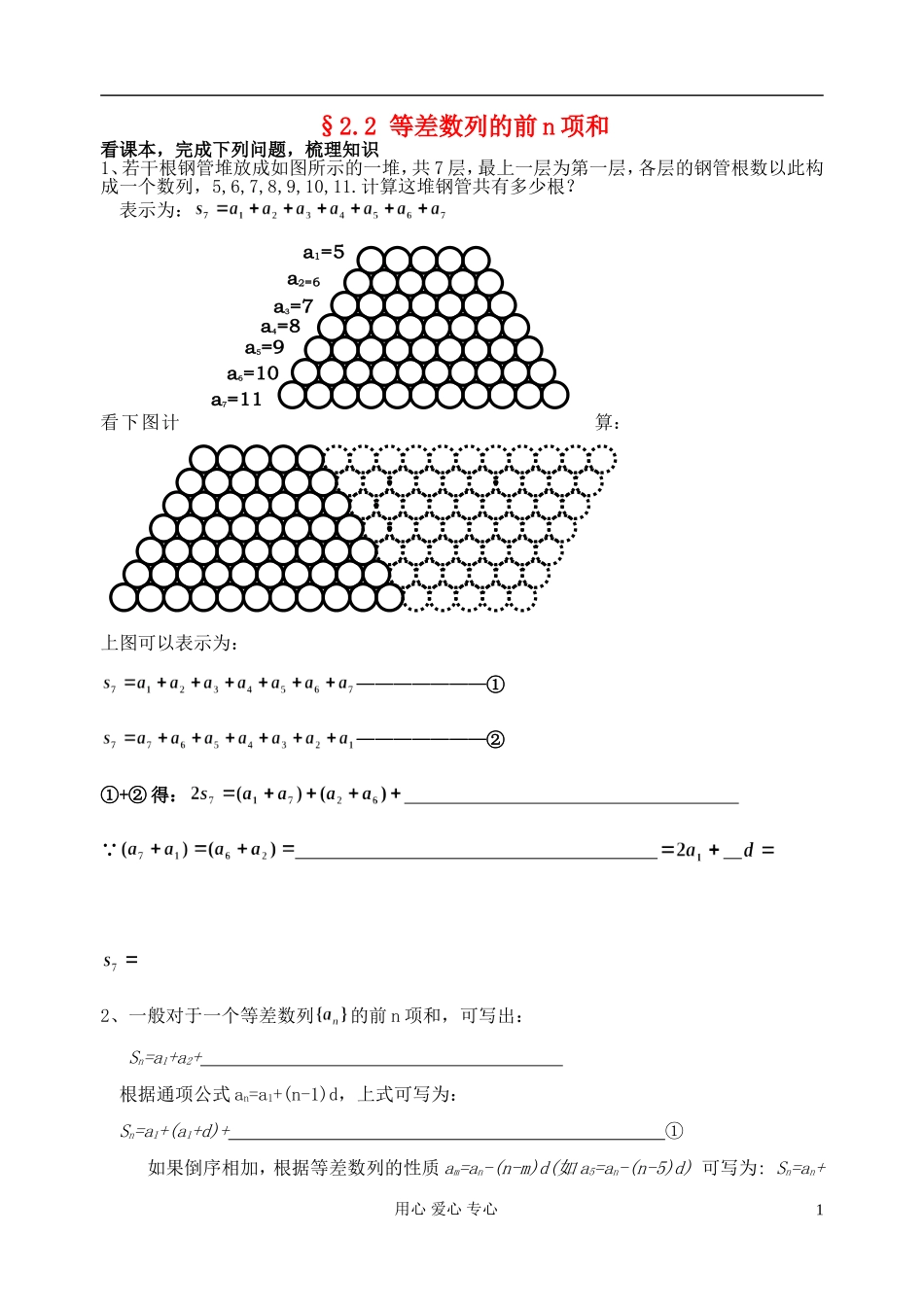
§2.2 等差数列的前 n 项和 看课本，完成下列问题，梳理知识1、若干根钢管堆放成如图所示的一堆，共 7 层，最上一层为第一层，各层的钢管根数以此构成一个数列，5,6,7,8,9,10,11.计算这堆钢管共有多少根？表示为：看下图计算：上图可以表示为：———————① ———————②①+② 得： 2、一般对于一个等差数列的前 n 项和，可写出： Sn=a1+a2+ 根据通项公式 an=a1+(n-1)d，上式可写为：Sn=a1+(a1+d)+ ① 如果倒序相加，根据等差数列的性质 am=an-(n-m)d(如 a5=an-(n-5)d) 可写为: Sn=an+用心 爱心 专心1a6=10a7=11a5=9a4=8a3=7a2=6a1=5(an-d)+ ②把①、②两等式两边分别相加，得2Sn==∴Sn=联想记忆，梯形的面积 S=，分别是体形的上底，下底和高，在等差数列中， 可以看成是梯形的面积 S， 可以看成是梯形的上底， 可以看成是梯形的下底， 可以看成是梯形的高.根据等差数列通项公式 an=a1+(n-1)d，前 n 项和 Sn可以由 a1,d,和 n 表示为： Sn=3、等差数列的性质:① 若数列 na是等差数列， nS 是其前 n 项的和，*Nk ，那么kS ，kkSS2，kkSS23 成等差数列新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆如下图所示：kkkkkSSSkkSSkkkaaaaaaaa3232k31221S321证明：② 奇数项和与偶数项和的关系：设数列 na是等差数列， 奇S是奇数项的和， 偶S是偶数项项的和，nS是前 n 项的和，则有如下性质前 n 项的和偶奇SSSn当 n 为偶数时，d2nS奇偶S，其中 d 为公差；证明：用心 爱心 专心2当 n 为奇数时，则中偶奇aS S，中奇a21nS，中偶a21nS，11SSnn偶奇，n偶奇偶奇偶奇SSSSSSSn（其中中a是等差数列的中间一项）证明：③、前 n 项和与通项的关系：若等差数列 na的前12 n项的和为12 nS，等差数列 nb的前12 n项的和为'12 nS，则'1212nnnnSSba基础自测1.记等差数列{an}的前 n 项和为 Sn，若 a1=，S4=20，则 S6等于 ( )A.16B.24C.36D.48 2.已知等差数列{an}中，前 n 项和为 Sn，若 a3+a9=6,则 S11等于（ ） A.12 B.33C.66 D.11 3.已知...