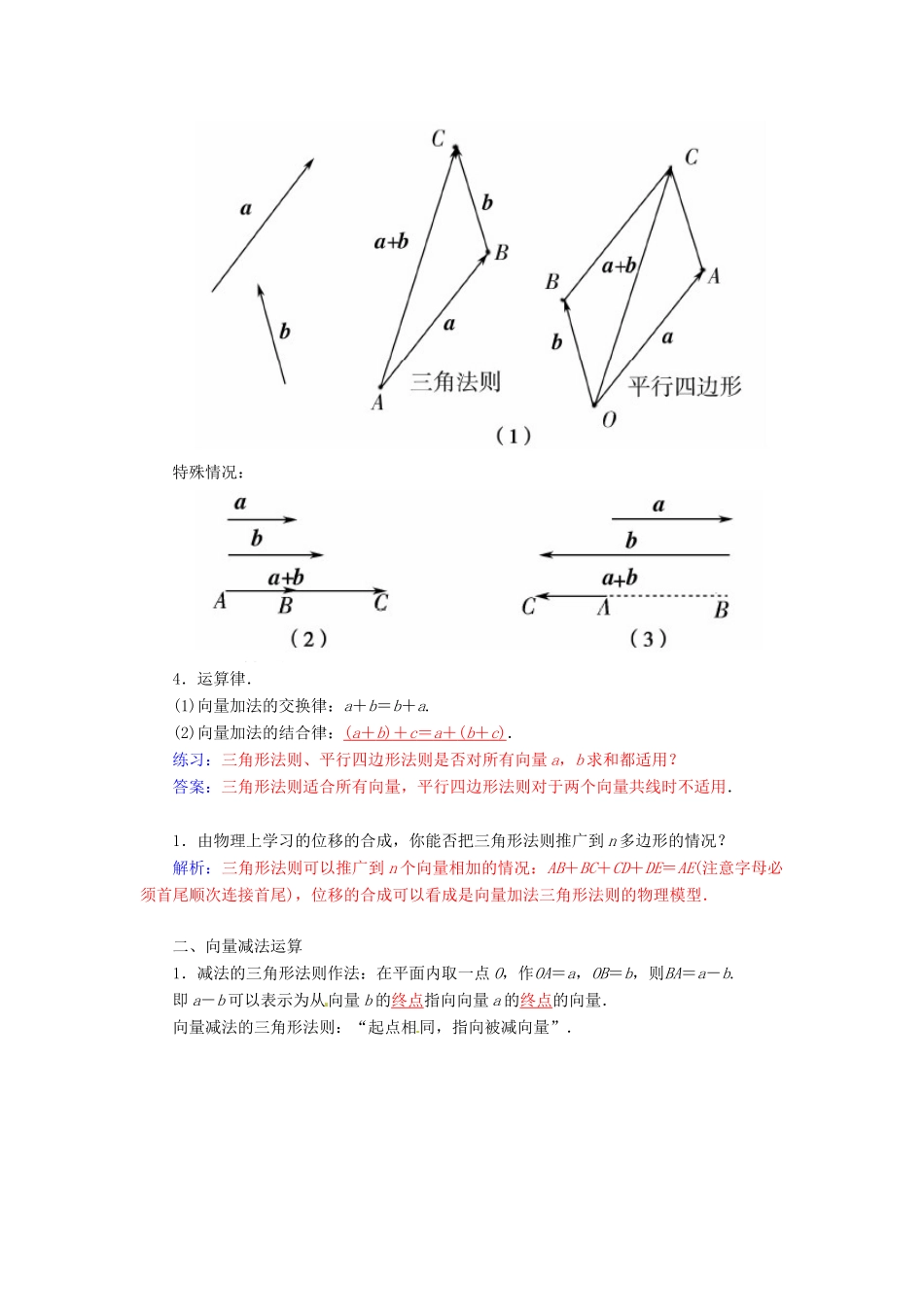
第二章 平面向量2.2 平面向量的线性运算2.2.1~2.2.2 向量加法、减法运算及其几何意义1.理解向量的和,掌握向量加法的三角形法则和平行四边形法则,向量加法的运算律及向量减法的三角形法则.2.理解向量模的性质.一、向量加法运算1.向量加法的定义:我们把求两个向量 a,b 和的运算,叫做向量的加法,记作:a+b.(1)两个向量的和仍然是一个向量;(2)零向量与任一向量 a 有 a+0=0+a=a.2.向量加法的三角形法则:向量AB与BC相加时,AB的终点作为BC的起点,这时起点 A到终点 C 的向量AC就是这两个向量的和向量,即AB+BC=AC.这种求向量和的方法叫三角形法则.向量加法的三角形法则:“首尾相接,首尾相连” .3.向量加法的平行四边形法则(对于两个向量共线不适用):以同一点 O 为起点的两个已知向量 a,b 为邻边作▱OACB,则以 O 为起点的对角线OC就是向量的和.这种作两个向量和的方法叫做向量加法的平行四边形法则,如图:特殊情况:4.运算律.(1)向量加法的交换律:a+b=b+a.(2)向量加法的结合律:( a + b ) + c = a + ( b + c ) .练习:三角形法则、平行四边形法则是否对所有向量 a,b 求和都适用?答案:三角形法则适合所有向量,平行四边形法则对于两个向量共线时不适用.1.由物理上学习的位移的合成,你能否把三角形法则推广到 n 多边形的情况?解析:三角形法则可以推广到 n 个向量相加的情况:AB+BC+CD+DE=AE(注意字母必须首尾顺次连接首尾),位移的合成可以看成是向量加法三角形法则的物理模型.二、向量减法运算1.减法的三角形法则作法:在平面内取一点 O,作OA=a,OB=b,则BA=a-b.即 a-b 可以表示为从向量 b 的终点指向向量 a 的终点的向量.向量减法的三角形法则:“起点相同,指向被减向量”.2.|a+b|、|a-b|、|a|+|b|、|a|-|b|之间的关系.对于任意的两个向量 a 与 b,有≤≤+.注意:当 a,b 共线时(包括同向和反向)上式等号成立.2.前面讨论的是向量运算,我们还学过那些运算?体会它 们的异同.解析:我们学过实数间的运算、集合间的运算、函数间的运算,今天又学到了向量间的运算.对于两个向量,通过三角形法则或平行四边形法则,有唯一的和向量与之对应.一般的,对于两个对象,通过一个法则都有唯一确定的对象与之对应,这就是运算.运算可以帮助我们解决很多的问题.1.下列等式正确的个数是(C)①a+0=a; ② b+a=a+b; ③...