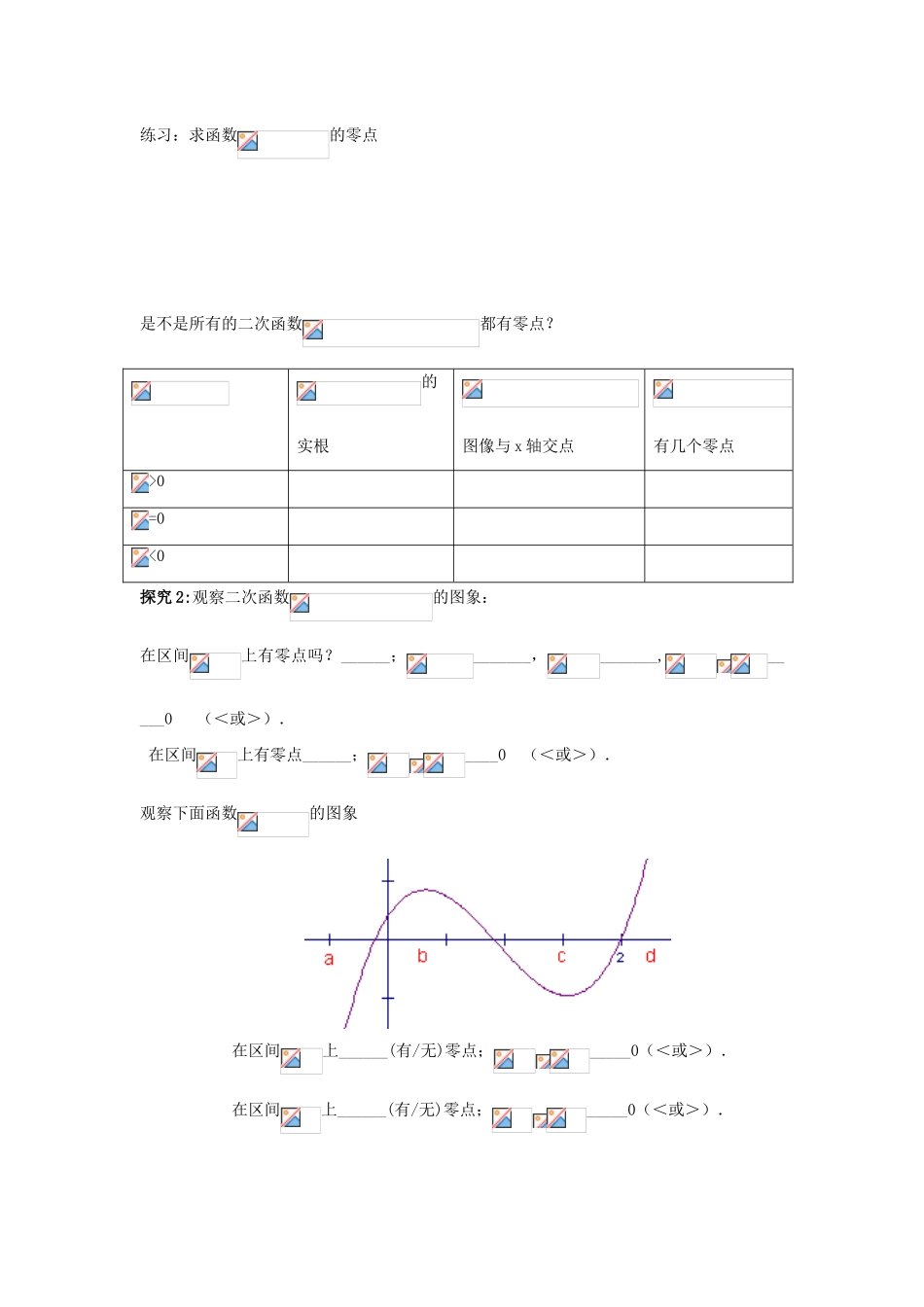
《方程的根与函数的零点》学习目标:1.掌握函数零点的概念;了解函数零点与方程根的关系; 2 零点的概念及零点存在性的判定学习难点:探究判断函数的零点个数和所在区间的方法.预习案:先来画出几个具体的一元二次方程对应的二次函数的图象,并观察二次函数与 x轴交点个数?方程与函数;方程与函数;方程与函数 填下表?函数函数图象函数与 x 轴交点f(x)=0 的根探究案:探 究 1 : 对 于 函 数, 把 使成 立 的 实 数叫 做 函 数的零点。注意:①函数零点不是一个点,而是具体的自变量的取值;②存在性一致:方程 f(x)=0有实数根⇔函数 y=f(x)的图象与 x 轴有交点⇔函数 y=f(x)有零点.零点是针对函数而言的,根是针对方程而言的。练习:求函数的零点是不是所有的二次函数都有零点?的实根图像与 x 轴交点有几个零点>0=0<0探究 2:观察二次函数的图象:在区间上有零点吗?______;_______,_______,_____0 (<或>). 在区间上有零点______;____0 (<或>).观察下面函数的图象 在区间上______(有/无)零点;_____0(<或>). 在区间上______(有/无)零点;_____0(<或>). 在区间上______(有/无)零点;_____0(<或>)._____0(<或>).在区间上______(有/无)零点? 0(<或>)。思考:若函数满足,在区间上一定有零点吗?若函数满足,在区间上一定有零点吗?由以上两步探索,你可以得出什么样的结论?1、判断下列结论是否正确,若不正确,请使用函数图象举出反例:(1)已知函数 y=f(x)在区间[a,b]上连续,且 f(a)·f(b)<0,则 f(x)在区间(a,b)内有且仅有一个零点。( )(2)已知函数 y=f(x)在区间[a,b]上连续,且 f(a)·f(b)≥0,则 f(x)在区间(a,b)内没有零点。( )(3)已知函数 y=f(x)在区间[a,b]满足 f(a)·f(b)<0,则 f(x)在区间(a,b)内存在零点。 ( )2.求函数 f(x)=lnx+2x-6 零点的个数。课堂总结当堂检测:1 求下列函数的零点:(1); (2)2.若函数 y=f(x)的图象是连续不断的,且 f(0)>0, f(1)f(2)f(4)<0,则下列命题正确的是 ( ) A.函数 f(x)在区间(0,1)内有零点 B.函数 f(x)在区间(1,2)内有零点 C.函数 f(x)在区间(0,2)内有零点 D.函数 f(x)在区间(0,4)内有零点3.函数的零点所在的区间是( )(A) (0,) (B)(,1)(C)(1,) (D)(,1)4.若函数 f(x)=ax+b 有一个零点 2,求函数 g(x)=bx2-ax 的零点