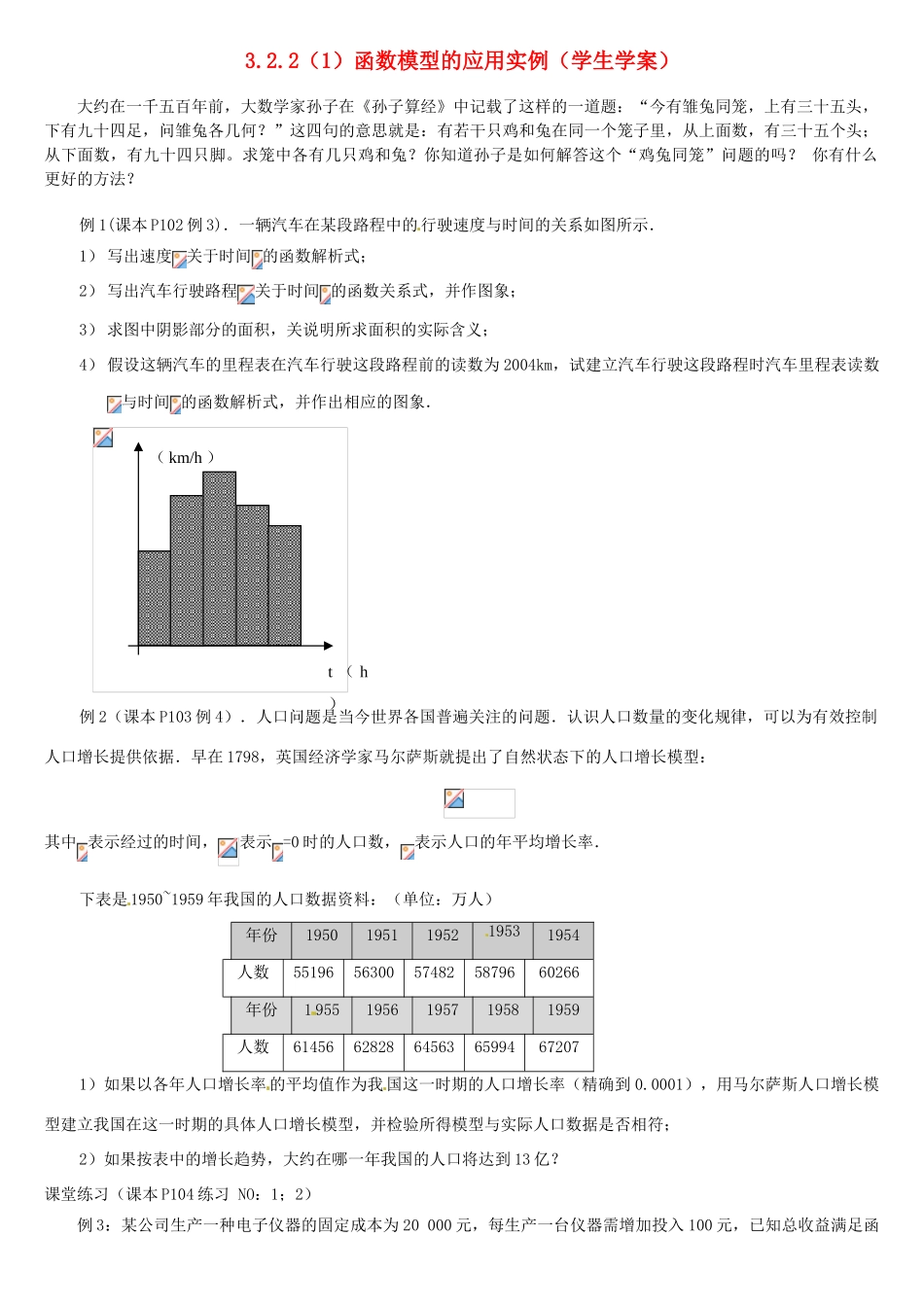
3.2.2(1)函数模型的应用实例(学生学案)大约在一千五百年前,大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?你知道孙子是如何解答这个“鸡兔同笼”问题的吗? 你有什么更好的方法?例 1(课本 P102 例 3).一辆汽车在某段路程中的行驶速度与时间的关系如图所示.1) 写出速度关于时间 的函数解析式;2) 写出汽车行驶路程关于时间 的函数关系式,并作图象;3) 求图中阴影部分的面积,关说明所求面积的实际含义;4) 假设这辆汽车的里程表在汽车行驶这段路程前的读数为 2004km,试建立汽车行驶这段路程时汽车里程表读数与时间 的函数解析式,并作出相应的图象.例 2(课本 P103 例 4).人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在 1798,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:其中 表示经过的时间,表示 =0 时的人口数,表示人口的年平均增长率.下表是1950~1959 年我国的人口数据资料:(单位:万人)年份19501951195219531954人数5519656300574825879660266年份1 9551956195719581959人数61456628286456365994672071)如果以各年人口增长率 的平均值作为我 国这一时期的人口增长率(精确到 0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;2)如果按表中的增长趋势,大约在哪一年我国的人口将达到 13 亿?课堂练习(课本 P104 练习 NO:1;2)例 3:某公司生产一种电子仪器的固定成本为 20 000 元,每生产一台仪器需增加投入 100 元,已知总收益满足函( km/h )t ( h)数:R(x)=.其中 x 是仪器的月产量.(1)将利润表示为月产量的函数 f(x);(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)四、布置作业:A 组:1.一个高为 H,盛水量为 V0 的水瓶的轴截面如图所示,现以均匀速度往水瓶中灌水,直到灌满为止,如果水深 h 时水的体积为 V,则函数 V=f(h)的图象大致是( )2 用清水洗衣服,若每次能洗去污垢的,要使存留的污垢不超过 1%,则至少要洗的次数是( )A.3 B.4 C.5 D.63(课本 P107 习题...