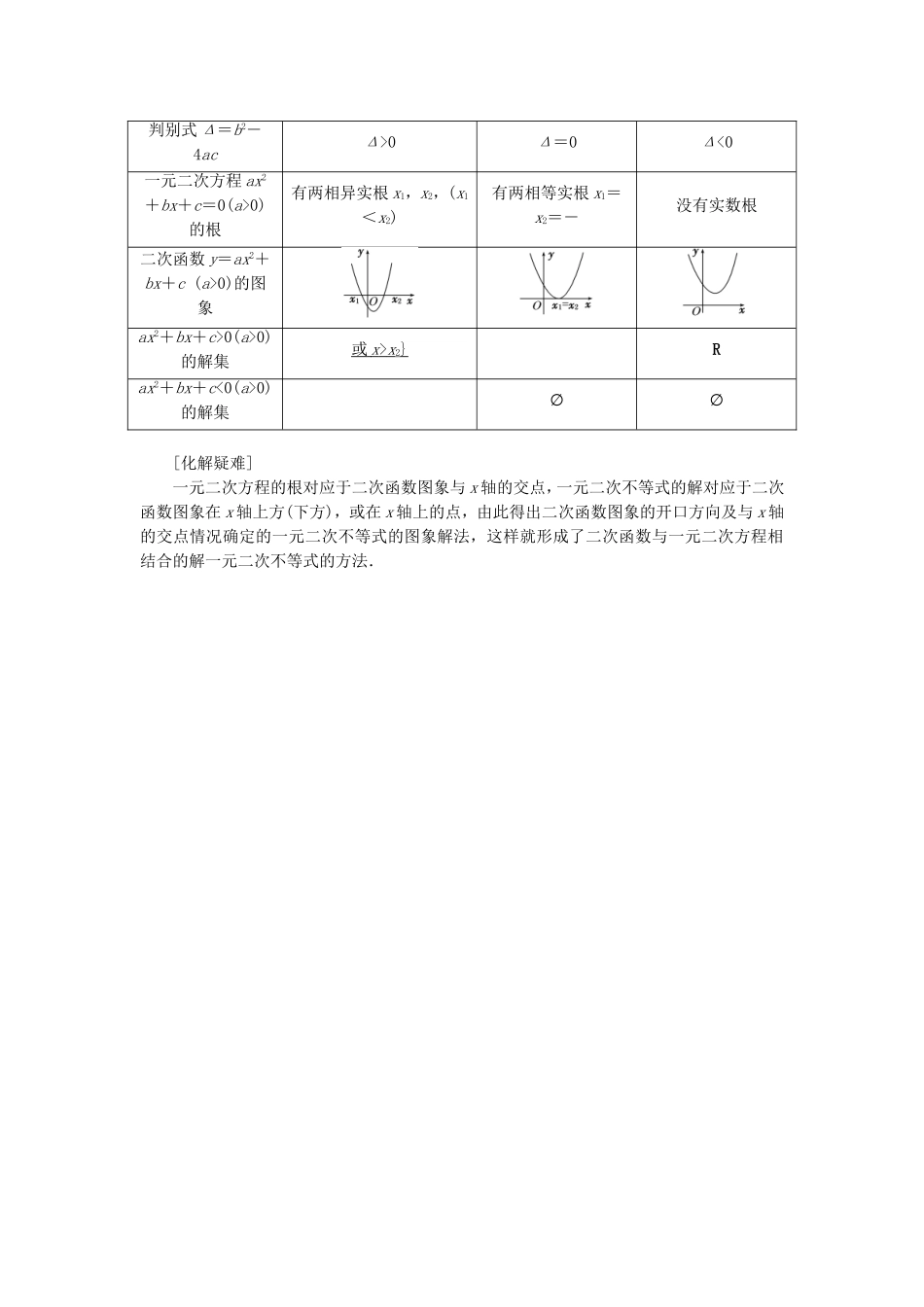
第三章第二节:一元二次不等式及其解法学习目标:理解一元二次不等式的概念及其与二次函数、一元二次方程的关系。初步树立“数形结合次函数、一元二次方程的关系。学法指导:发现、讨论法;数形结合。 ”的观念。掌握一元二次不等式的解法及步骤。学习重点、难点:一元二次不等式、二次函数、一元二次方程的关系;一元二次不等式的解法及其步骤。知识链接:一元二次不等式的概念[提出问题]观察下列不等式:(1)x2>0;(2)-x2-2x≤0;(3)x2-5x+6>0.问题 1:以上给出的 3 个不等式,它们含有几个未知数?未知数的最高次数是多少?提示:它们只含有一个未知数,未知数的最高次数都是 2.问题 2:上述三个不等式在表达形式上有何共同特点?提示:形如 ax2+bx+c>0(或≤0),其中 a,b,c 为常数,且 a≠0.[导入新知]1.一元二次不等式我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式,即形如 ax2+bx+c>0(≥0)或 ax2+bx+c<0(≤0)(其中 a≠0)的不等式叫做一元二次不等式.2.一元二次不等式的解与解集使一元二次不等式成立的 x 的值 ,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的解集. [化解疑难]1.定义的简单应用:判断一个不等式是否为一元二次不等式,应严格按照定义去判断,即未知数只有 1 个,未知数的最高次数是 2,且最高次的系数不能为 0.2.解集是解的集合,故一元二次不等式的解集一定要写成集合或区间的形式.一元二次不等式的解法[提出问题]已知:一元二次函数 y=x2-2x,一元二次方程 x2-2x=0,一元二次不等式 x2-2x>0.问题 1:试求二次函数与 x 轴交点坐标提示:(0,0)、(2,0)问题 2:一元二次方程根是什么?提示:x1=0,x2=2.问题 3:问题 1 中的坐标与问题 2 中的根有何内在联系?提示:交点的横坐标为方程的根.问题 4:观察二次函数图象,x 满足什么条件,图象在 x 轴上方?提示:x>2 或 x<0.问题 5:能否利用问题 4 得出不等式 x2-2x>0,x2-2x<0 的解集?提示:能,不等式的解集为{x|x>2 或 x<0},{x|0<x<2}.[导入新知]一元二次不等式与相应的二次函数及一元二次方程的关系如表判别式 Δ=b2-4acΔ>0Δ=0Δ<0一元二次方程 ax2+bx+c=0(a>0)的根有两相异实根 x1,x2,(x1<x2)有两相等实根 x1=x2=-没有实数根二次函数 y=ax2+bx+c (a>0)的图象ax2+bx+c>0(a>0)的解集或 x > x 2}...