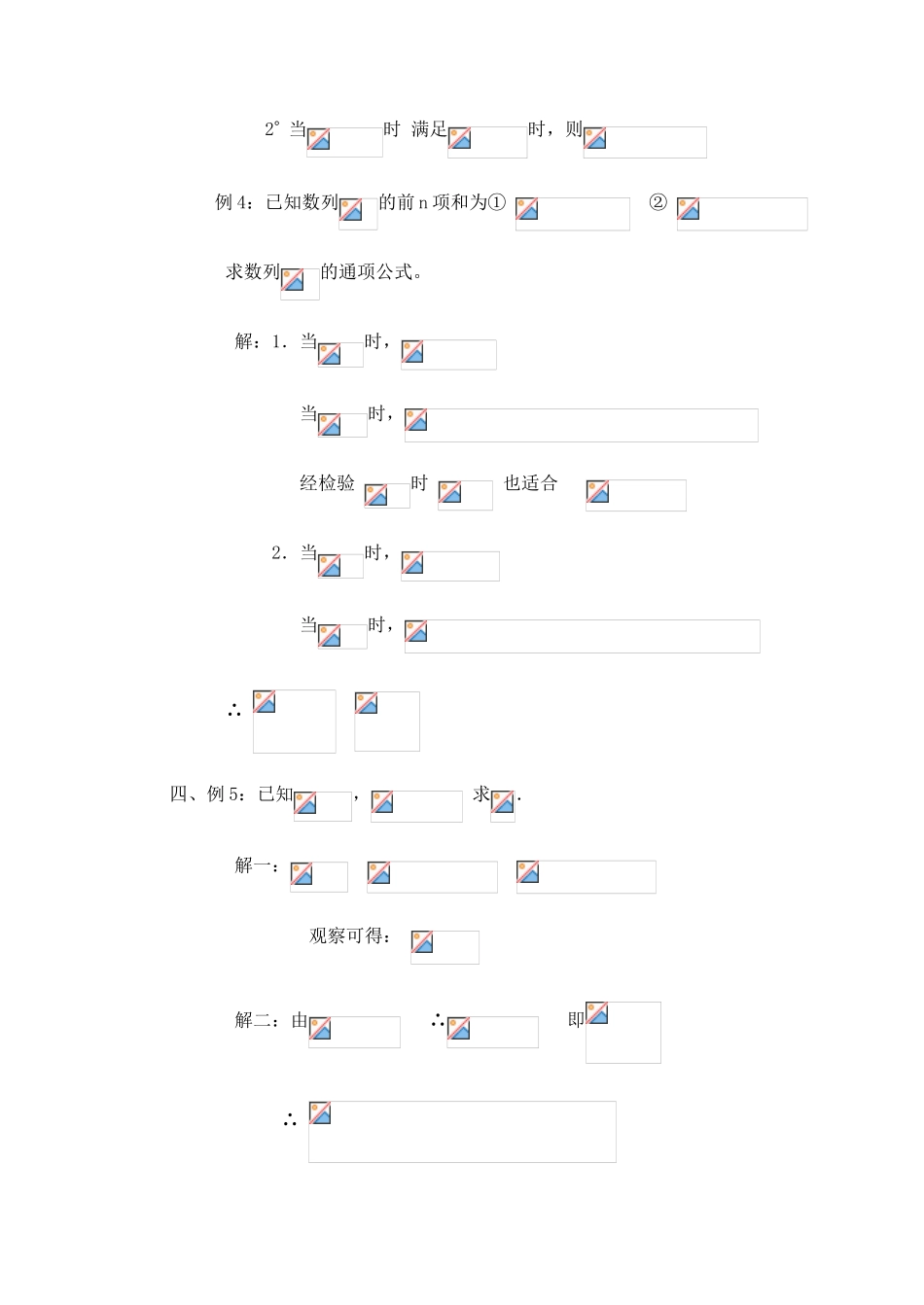
§3.1.2 数列的递推关系目的:1. 数列递推公式的概念;2.会根据给出的递推公式写出数列的前 n 项。重点: 数列的任意连续若干项能满足的关系式称为该数列的一个递推公式,由递推公式和相应有尽有前若干项可以确定一个数列.这种表示方法叫做递推公式法或递推法.难点: 1.根据数列的首项和递推公式写出它的前几项,关归纳出通项公式. 2.的关系 过程:一、 复习:数列的定义,数列的通项公式的意义(从函数观点出发去刻划)二、递推公式 (见课本 P112-113 略) 上一节课钢管的例子 从另一个角度,可以: “递推公式”定义:已知数列的第一项,且任一项与它的前 一项(或前项)间的关系可以用一个公式来表示,这个公式就叫 做这个数列的递推公式。 例 1: (P113 例三)略 例 2: 已知, 求. 解一:可以写出:,,,,…… 观察可得: 解二:由题设: ∴ ∴ 三、例 3 : 若 记 数 列的 前 n 项 之 和 为 Sn 试 证 明 : 证:显然时 ,当即时 ∴ ∴ 注意:1 此法可作为常用公式 2 当时 满足时,则例 4:已知数列的前 n 项和为① ② 求数列的通项公式。 解:1.当时, 当时, 经检验 时 也适合 2.当时, 当时, ∴ 四、例 5:已知, 求. 解一: 观察可得: 解二:由 ∴ 即 ∴ ∴ 五、小结:递推公式 (简单阶差、阶商法) 由数列和求通项 六、作业:P114 习题 3.1 3、4 七、练习:1. 根据下面数列{an}的首项和递推公式写出它的前 4 项。并归纳出通项公式。(1)a1=1,an+1=1+an (n≥1)(2)a1=0, an+1= an+(2n-1)(n∈N*)2. 已知数列{an}满足 a1=2,a2=5,a4=23,且 an+1=αan+β,求实数 α、β 的值。3.已知,(),求的值。4.已知数列{an}的前 n 项和,试求其通项 an5.已知数列{an}的前 n 项和为 n2+Pn 数列{bn}的前 n 项和为 3n2-2n.(1) 若 a10=b10,求 P 的值;(2) 取数列{bn}的第 1 项,第 3 项,第 5 项,…,构成一个新数列{cn},求数列{cn}的通项。6.设 a1=2,an+1=2an+3,则通项 an 可能是 ( ) A 5-3n B 3•2n-1-1 C5-3n2 D 5•2n-1-37.设 an=-n2+10n+11,则数列{an}从首项到第( )项的和最大。 A 10 B 11 C 10 或 11 D 128.在数列{an}中,a1=a2=2,且 an+2=3an+1-an,(n∈N*),则 a5= 9. 在数列{an}中,,a1=1,an+1=( n∈N*)则是这个数列的第 项10.已知数列{an}的前 n 项和 Sn=n3+1,试求其通项 an11.数列{an},{bn}的首项都是 1,且符合规律 a1+b1=a2,b1+a2=b2,a2+b2=a3,b2+a3=b3, …, 试求 an+1,bn+1的表达式,并求 a4与 b4。12.在数列{an}中,an=,且 S=9,求 n。13.设{an}是首项为 1 的正项数列,且(n∈N*),则它的通项公式 an= 14 . 已 知 数 列 {an} 中 , a1=1 , 数 列 {bn} 中 , b1=0, 当 n≥2 时 , ,求 an, bn