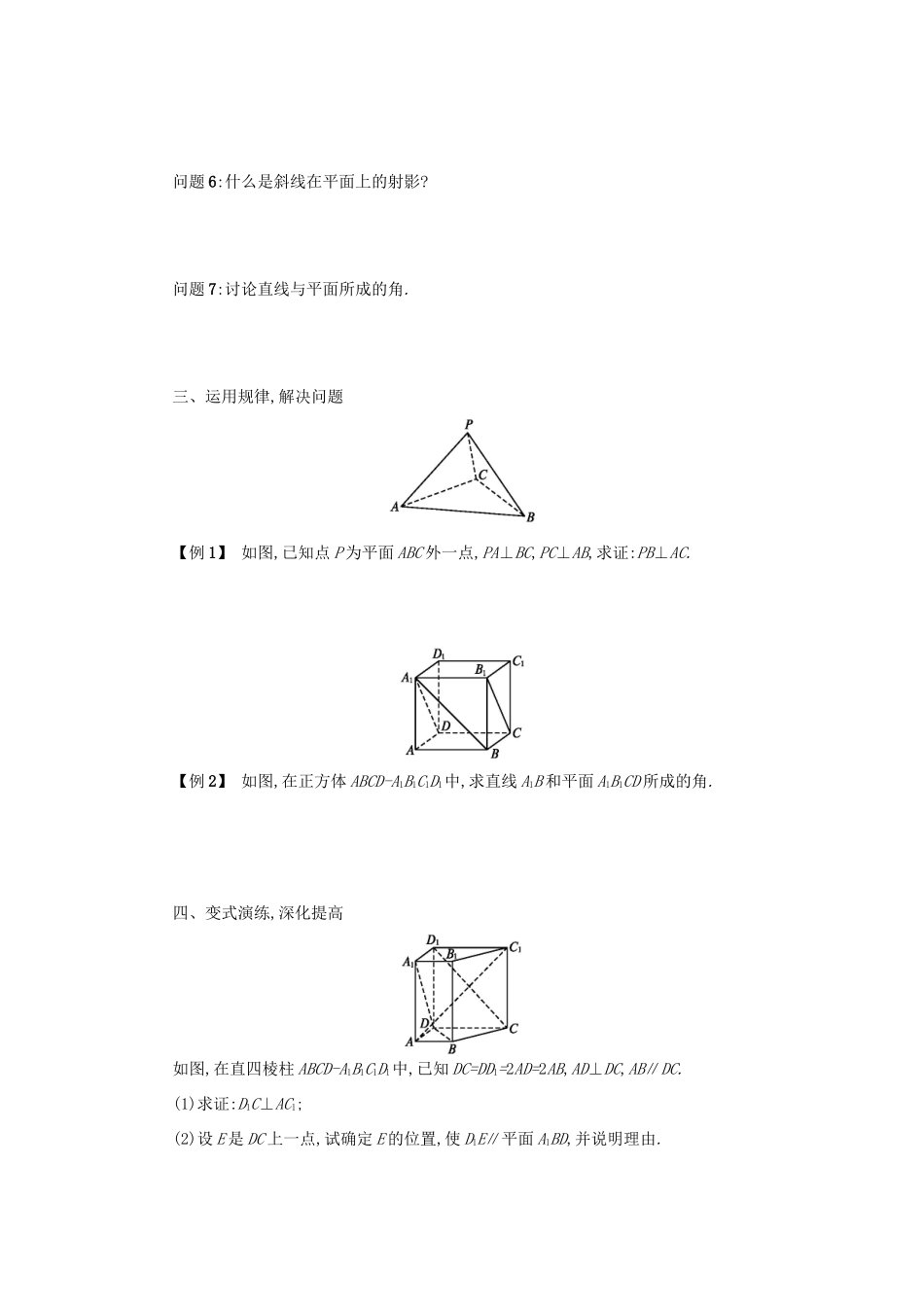
第二章 点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定学习目标1.探究直线与平面垂直的判定定理,培养学生的空间想象能力.2.掌握直线与平面垂直的判定定理的应用,培养学生分析问题、解决问题的能力.3.让学生明确直线与平面垂直在立体几何中的地位.合作学习一、设计问题,创设情境日常生活中,我们对直线与平面垂直有很多感性认识,比如,旗杆与地面的位置关系,大桥的桥柱与水面的位置关系等,都给我们以直线与平面垂直的印象.问题 1:如果一条直线垂直于一个平面的无数条直线,那么这条直线是否与这个平面垂直?举例说明.二、信息交流,揭示规律问题 2:借助生活中垂直的含义,能不能说出直线与平面垂直的定义?问题 3:如何画直线与平面垂直?问题 4:如图,请同学们准备一块三角形的纸片,我们一起做一个试验:过△ABC 的顶点 A翻折纸片,得折痕 AD,将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).(1)折痕 AD 与桌面垂直吗?(2)如何翻折才能使折痕 AD 与桌面所在的平面 α 垂直?问题 5:如何判定直线和平面平行呢?问题 6:什么是斜线在平面上的射影?问题 7:讨论直线与平面所成的角.三、运用规律,解决问题【例 1】 如图,已知点 P 为平面 ABC 外一点,PA⊥BC,PC⊥AB,求证:PB⊥AC.【例 2】 如图,在正方体 ABCD-A1B1C1D1中,求直线 A1B 和平面 A1B1CD 所成的角.四、变式演练,深化提高如图,在直四棱柱 ABCD-A1B1C1D1中,已知 DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.(1)求证:D1C⊥AC1;(2)设 E 是 DC 上一点,试确定 E 的位置,使 D1E∥平面 A1BD,并说明理由.五、反思小结,观点提炼请同学们总结下本节课所学习内容:六、作业精选,巩固提高课本 P67练习第 1,2,3 题.参考答案一、问题 1:在阳光下观察直立于地面的旗杆 AB 及它在地面的影子 BC.随着时间的变化,尽管影子 BC 的位置在移动,但是旗杆 AB 所在直线始终与 BC 所在直线垂直.也就是说,旗杆AB 所在直线与地面内任意一条不过点 B 的直线 B'C'也是垂直的.二、问题 2:一条直线和平面内的任何一条直线都垂直,我们说这条直线和这个平面互相垂直,直线叫做平面的垂线,平面叫做直线的垂面.过一点有且只有一条直线和一个平面垂直;过一点有且只有一个平面和一条直线垂直.平面的垂线和平面一定相交,交点叫做垂足.问题 3:直线和平面垂直的画法及表示如下:如图,表示方法为 a⊥α.问题 4:当且仅当折痕 AD 是 BC 边上的高时,AD 所在...