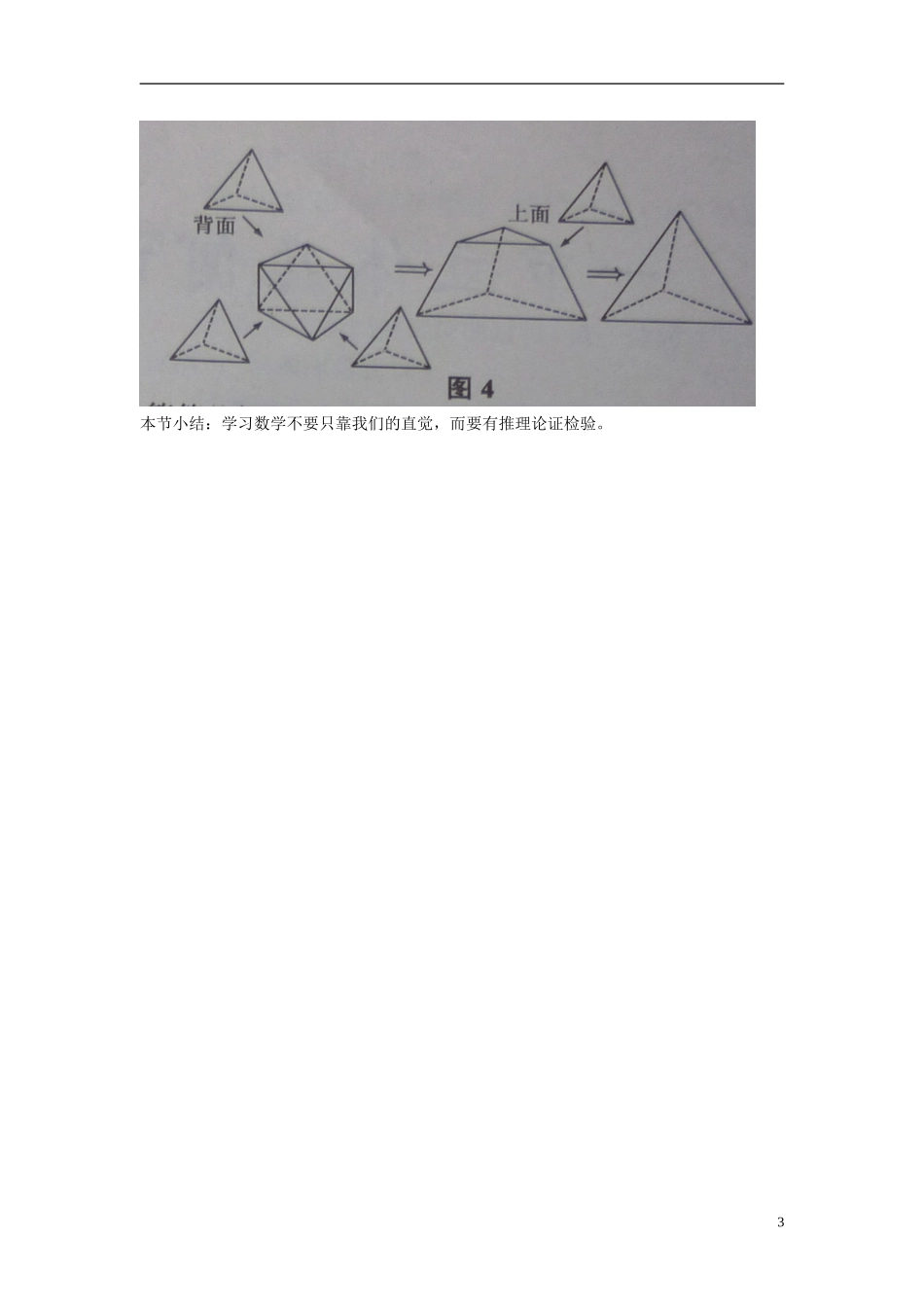
第 10 课时 立体几何趣题——正多面体拼接构成新多面体面数问题教学要求: 训练学生空间想象能力,动手动脑能力,提高学习数学兴趣教学过程:一、问题提出在《数学(高二下册)》“立体几何多面体”一节的课堂教学中,老师给出了一道例题:“已知一个正四面体和一个正八面体的棱长都相等,把它们拼接起采,使一个表面重合,所得的新多面体有多少个面?”对于这个问题学生们表现出了极大的兴趣.他们通过直观感知,提出了自己的看法:正四面体和正八面体共 12 个面,两者各有一个面重叠,因此减少两个面,所以重合之后的新多面体有 10 个面. 二、故事介绍 教师乘着学生浓厚的兴趣讲了一个与这道例题有关的故事.多年前美国的一次数学竞赛中有这样一道题:一个正三棱锥和一个正四棱锥,所有棱长都相等,问重合一个面后还有几个面?大学教授给这道竞赛题的参考答案是 7 个面,他们认为正三棱锥和正四棱锥共 9 个面,两者各有 一个面重叠,减少两个面,所以重合之后还有 7 个面。但佛罗里达州的一名参赛学生丹尼尔的答案是 5 个面,与参考答案不合而被判错误,对此丹尼尔一直有所疑惑,于是他动手拼接了符合题意的正三棱锥和正四棱锥实物模型,结果正如他所判断的只有 5 个面;他将自己的结论和实物模型提交给竞赛组委会,教授们接受了他的想法并改正了这道题的答案。 三、操作确认 故事讲完后学生立刻对丹尼尔的结论进行了激烈地讨论.于是教师建议:请同学们拿出课前分组做出上述两个问题的实物模型,通过自己的操作(模型组合)来确认自己的结论.学生展示大小不一的实物模型.教师让每个组的学生代表在讲台上演示实物模型的组合过程.通过观察、讨论,全班同学明白丹尼尔结论的原因所在.同时也观察到了正四面体和正八面体重合之后新多面体只有七个面,这与学生们在上一节课通过直观感知所得的结论是不一致的。原因在于他们发现在重合过程中正四面体和正八面体另有两个侧面分别拼接成一个面了. 四、思辩论证老师要求学生利用立体几何的相关知识,对操作实物模型得出的结论进行证明。学生对照实物模型提出了证明思路:将正八面体和正四面体拼接的两个侧面想象成两个半平面拼接成一个平面即表示这两个半平面所构成的二面角为.证明如下:如图 1,在正八面体 AC 中,连结 AC 交平面 BE 于点O.设正八面体的棱长为 1,BF 的中点为 D,连结AD 、CD,易得∠ADC 为二面角 A―BF―C 的平面角 。AD=DC=,AC=2AO=由 余 ...