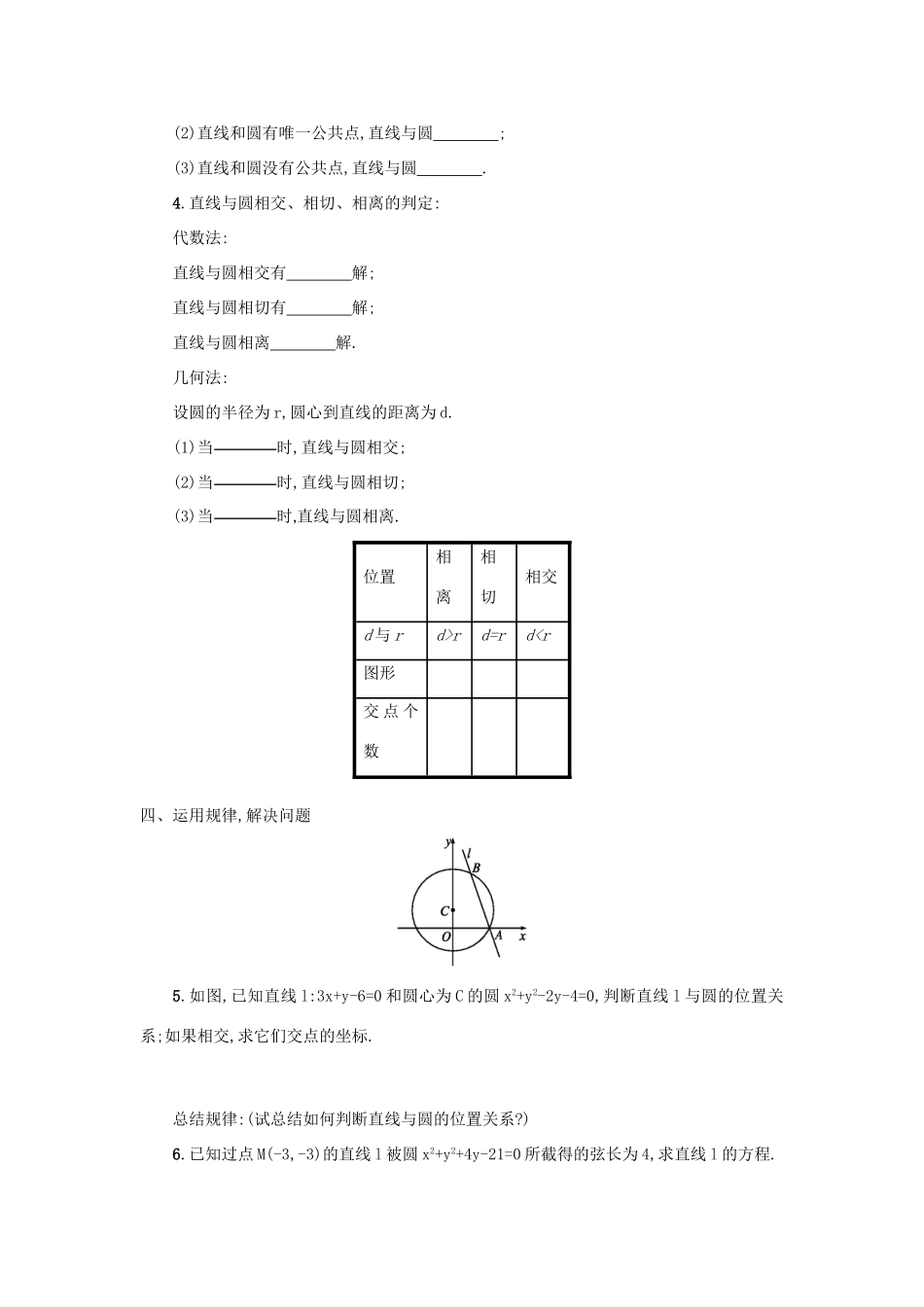
第四章 圆与方程4.2 直线、圆的位置关系4.2.1 直线与圆的位置关系学习目标1.理解直线与圆的位置关系.2.利用点到直线的距离公式求圆心到直线的距离.3.会判断直线与圆的位置关系.学习过程一、设计问题,创设情境一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为 30 km 的圆形区域.已知小岛中心位于轮船正西 70 km 处,港口位于小岛中心正北 40 km 处.如果轮船沿直线返港,那么它是否会有触礁危险?问题 1:初中学过的平面几何中,直线与圆的位置关系有几类?问题 2:在初中,我们怎样判断直线与圆的位置关系?二、学生探索,尝试解决如何通过代数的方法来研究直线与圆的这三种位置关系.1.从方程的角度来看:直线与圆相交,有两个公共点,组成的方程组应该有 个解. 直线与圆相切,有一个公共点,组成的方程组应该有 个解. 直线与圆相离,没有一个公共点,组成的方程组应该 解. 从初中直线与圆相切,常用到的作辅助线的方法来讲,连接切点和圆心得到半径,即圆心到直线的距离等于半径.2.一般地,已知直线 Ax+By+C=0(A,B 不同时为零),和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为 d= ,则 d 与半径 r 有下面三种关系:dr. 三、信息交流,揭示规律3.直线与圆相交、相切、相离的定义:(1)直线和圆有两个公共点,直线与圆 ; (2)直线和圆有唯一公共点,直线与圆 ; (3)直线和圆没有公共点,直线与圆 . 4.直线与圆相交、相切、相离的判定:代数法:直线与圆相交有 解; 直线与圆相切有 解; 直线与圆相离 解. 几何法:设圆的半径为 r,圆心到直线的距离为 d.(1)当时,直线与圆相交;(2)当时,直线与圆相切;(3)当时,直线与圆相离.位置相离相切相交d 与 rd>rd=rd